Задача 35168 ...

marinacus

2019-03-31 23:17:27

В параллелепипеде ABCDA1B1C1D1 со стороной основания 4 и боковым ребром 3 отмечены точки M ∈ A1B1, N ∈ B1С, такие, что A1M : MB1, = C1N : NB1 = 1 : 3.

1. Постройте сечение плоскостью DMN и найдите:
2. угол между плоскостью сечения и плоскостью основания
3. площадь сечения,
4. площадь проекции сечения на плоскость ABC,.

В кубе ABCDA1B1C1D1 со стороной 4 отмечена точка M ε AB так, что AM : MB = 1 : 3

5. Найдите расстояние между прямыми DM и CB1
6. Найдите расстояние между прямыми DM и DB.

sova

2019-04-01 11:07:23

1) Cм. рис.
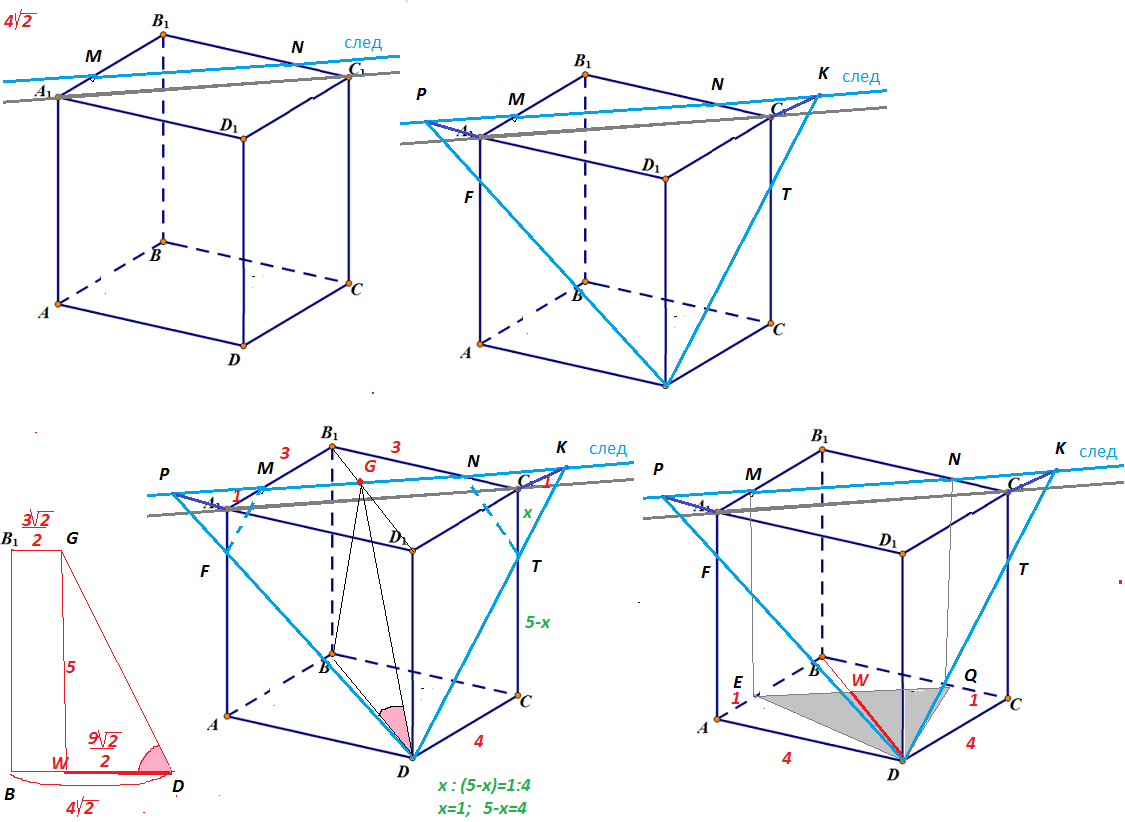
Сечение [b]пятиугольник DFMNT[/b]
2)
Из прямоугольной трапеции ВВ_(1)GD( cм. рисунок):
BB_(1)=5
B_(1)G=3sqrt(2)/2
BD=4sqrt(2)
WD=BD-BW=BD-B_(1)G=4sqrt(2)- (3sqrt(2)/2)= [b]9sqrt(2)/2[/b]

tg ∠ GBD= 5/(9*sqrt(2)/2)=10/(9*sqrt(2))= [b]5sqrt(2)/9[/b]

∠ GBD= [b]arctg (5sqrt(2)/9)[/b]

3) S_(cечения)=S_( Δ DPK)- S_( ΔNKT)-S_( ΔMPF).

Δ DPK - равносторонний
DP=PK=DK=5sqrt(2)
ΔNKT= ΔMPF
NK=KT=NT=MP=PF=MF=sqrt(2)

S_(равностороннего треугольника со стороной а)=a^2*sqrt(3)/4

S_(cечения)=(5sqrt(2))^2- (sqrt(2))^2 - (sqrt(2))^2) * sqrt(3)/4=

=(50-2-2)*sqrt(3)/4=46sqrt(3)/4= [b]23sqrt(3)/2[/b]

4) DEQ - проекция пятиугольника DFMNT на плоскость АВСD

S_(DEQ)= (1/2)EQ*WD=(1/2)*(3sqrt(2)) * (9sqrt(2))/2=

=27/2= [b]13,5[/b]