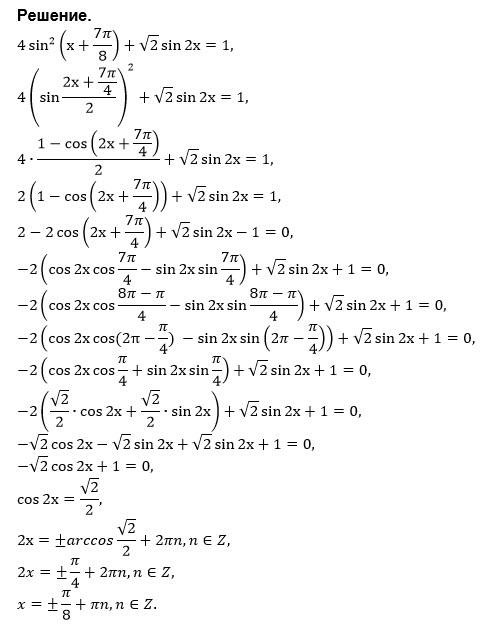Задача 35152 ...

vk349760626

2019-03-31 11:33:09

Решите уравнение 4sin^2(x+7π/8) + sqrt(2) sin2x=1
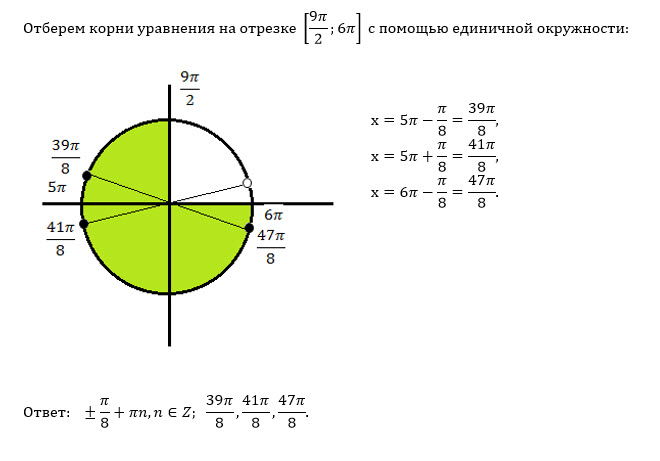
Укажите корни, принадлежащие отрезку [9π/2 ; 6π]

sova

2019-03-31 18:43:20

2sin^2(x+(7π/8))=1-cos(2x+(14π/8))=1-cos(2x+(7π/4))
4sin^2(x+(7π/8))=2-2cos(2x+(7π/4))

cos(2x+(7π/4))=cos2x*cos(7π/4) - sin2x*sin(7π/4)=

=cos2x*(sqrt(2)/2) - sin2x*(-sqrt(2)/2)=

=(sqrt(2)/2)*(cos2x+sin2x)


Уравнение:
2-sqrt(2)*(cos2x+sin2x)+ √2 sin2x=1

sqrt(2)*cos2x=1
cos2x=sqrt(2)/2

2x= ± (π/4)+2πn, n ∈ Z

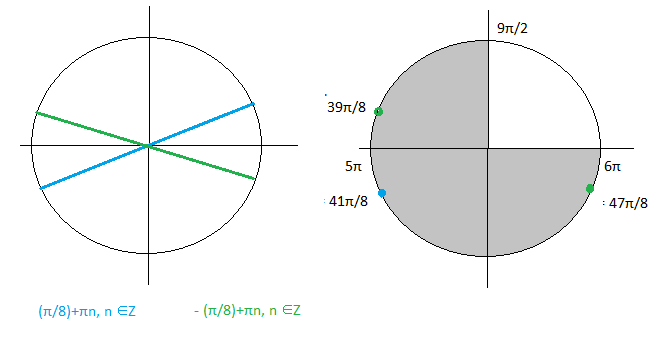
[b]x= ± (π/8)+πn, n ∈ Z[/b]

б)отрезку [9π/2 ; 6π]
принадлежат корни:
x=- (π/8)-π+6π= [b]39π/8[/b]
x= (π/8)-π+6π= [b]41π/8[/b]
x=- (π/8)+6π= [b]47π/8[/b]

см. рис.