Задача 3505 a) Решите уравнение...

slava191

02.09.2015

a) Решите уравнение sin3x=2cos(Pi/2-x)
б) Найдите все корни этого уравнения, принадлежащие промежутку (-3Pi/2; 0]

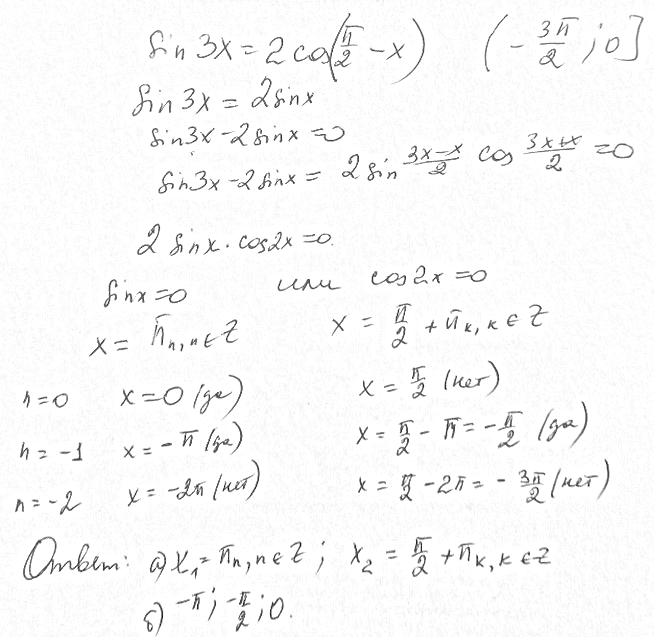
Ответ: В решение

vk397114329

27.03.2018

Решение:
sin3x=2cos(pi/2-x)
Так как sin3x=3sinx-4sin^3x. и cos(pi/2-x)=sinx. получаем:
3sinx-4sin^3x-2sinx=0. sinx-4sin^3x=0. sinx(1-4sin^2x)=0
1) sinx=0; x=pi*k. k -целое число.
2)1-4sin^2x=0. sin^2x=1/4. x=+-pi/6+pi*k. k-целое число.
Отберем корни принадлежащие полуинтервалу (-3pi/2;0]
1) x=pi*k. тогда -3pi/2 < pi*k < =0. -3/2 < k < =0. получаем два значения k:-1 и 0 и два корня -pi;и 0.
2) x=pi/6+pi*k. тогда -3pi/2 < pi/6+pi*k < =0. -5/3 < k < =-1/6. получаем k=-1 и один корень -5pi/6.
3) x=-pi/6+pi*k.тогда -3pi/2 < -pi/6+pi*k < =0. -4/3 < k < =1/6.получаем два значения к: -1 и о, и два корня -7pi/6; и -pi/6. Проверка показывает,что найденные значения принадлежат указанному полуинтервалу и являются решением исходного уравненияю
Ответ:
a)x=pi*k; x=+-pi/6+pi*k.k-целые числа.
b) корни уравнения: -pi;-7pi/6;-pi/6;0.