Задача 34919 ...

vk280770680

2019-03-25 18:11:23

Помогите решить
Решить уравнение log8x=-1
Упростить выражение sin3 a cos a + sin a cos 3 a
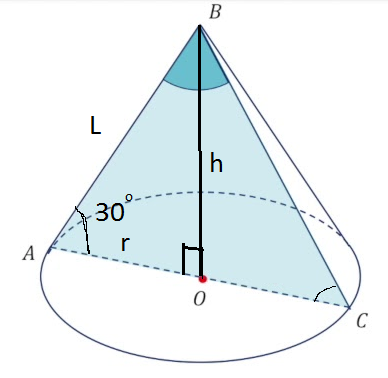
Угол между образующей и плоскостью основания конуса равен 30°, а радиус основания конуса 6√3см. Найти высоту конуса.

sova

2019-03-25 18:16:58

★

1.
x=8^(-1)
[b]x=1/8[/b]

2.

sin3 a cos a + sin a cos 3 a =синус суммы=sin(3a+a)=sin4a

3.

Высота конуса перпендикулярна плоскости основания.
h=L/2
L=2h
По теореме Пифагора
L^2-h^2=r^2

(2h)^2-h^2=r^2
3h^2=(6sqrt(3))^2
3h^2=108
h^2=36
[b]h=6 cм[/b]