Задача 34593 ...
Условие
1. Существует ли треугольник, у которого одна сторона 5 см, длина другой в сантиметрах является одним из корней уравнения x ∙ (5x – 19)(9x + 27) = 0, а длина третьей стороны составляет половину длины второй? Если да, то начертите такой треугольник.
2. Существует ли треугольник, у которого одна сторона 6,4 см, отношение двух других равно отношению корней уравнений 5x – (11 – 3x) = 6 ∙ (x – 1) и –4x = –50, а периметр треугольника равен 23,2 см? Если да, то начертите такой треугольник.
Вариант 4
1. Существует ли треугольник, у которого одна сторона 10 см, длина другой в сантиметрах является одним из корней уравнения x ∙ (5x – 27)(9x + 18) = 0, а длина третьей стороны составляет половину длины второй? Если да, то начертите такой треугольник.
2. Существует ли треугольник, у которого одна сторона 7,6 см, отношение двух других равно отношению корней уравнений 7 ∙ (1 – x) = 4x – (11 + 3x) и –4x = –6, а периметр треугольника равен 18,1 см? Если да, то начертите такой треугольник.
Все решения
Задача 1.
Решаем уравнение:
x*(5x-19)*(9x+27)=0
x=0 или 5х-19=0 или 9х+27=0
Корни уравнения:
х=0 или х=19/5=3,8 или х=-3
Сторона треугольника не может быть отрицательной или нулем, поэтому остается второй корень
х=3,8
Третья сторона по условию:
равна х/2=1,9
Чтобы треугольник существовал, необходимо выполнение неравенства треугольника:
каждая сторона должна быть меньше суммы двух других
( ломаная из двух звеньев больше расстояния между начальной и конечной точками)
1,9 < 3,8+5 - верно
3,8 < 1,9+5 - верно
5< 1,9+3,8 - верно
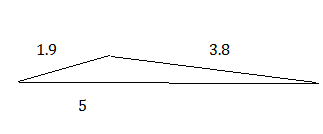
См. рис.
Задача 2.
5х-11+3х=6х-6
2х=5
х_(1)=2,5 - корень первого уравнения
-4x=-50
x_(2)=12,5 - корень второго уравнения
х_(2):х_(1)=12,5:2,5=5
a:b=5
a=5b
c=6,4
Р=a+b+c
5b+b+6,4=23,2
6b=16,8
b=2,8
a=5b=14
Треугольник не существует, так как не выполняется неравенство треугольника:
14 < 2,8+6,4 - неверно
Рисунок к задаче 1.