Задача 34557 ...

vk411719339

17 марта 2019 г. в 10:09

12. Найдите наибольшее значение функции [m] у = (x + 2)^{2}(x + 5) + 2 [/m] на отрезке [m] [ -5; -\frac{1}{2} ] [/m]

13. а) Решите уравнение 8sinxcos³x – 2sin2x – 2cos²x + 1 = 0.
б) Найдите все корни этого уравнения, принадлежащие промежутку [m] [ -\frac{3\pi}{2}; -2 ] [/m]

sova

18 марта 2019 г. в 10:45

y`=((x+2)<sup>2</sup>·(x+5)+2)`=((x+2)²)`·(x+5)+(x+2)<sup>2</sup>·(x+5)`+2`=
=2·(x+2)·(x+5)+(x+2)<sup>2</sup>·1+0=(x+2)·(2x+10+x+2)=(x+2)(3x+12)
y`=0
x=–2 или x=–4
оба значения принадлежат отрезку [–5;–1/2]
Находим знак производной.
y`=(x+2)(3x+12) – квадратичная функция, график парабола, ветви направлены вверх, расположена ниже оси Ох на (–4;–2)
Значит,
знак f`(x):
[–5] _+__ (–4) ___–__ (–2)__+__ [–1/2]
х=–2 – точка минимума

x=–4 – точка максимума.

Находим значение в этой точке и в правой концевой точке отрезка и выбираем наибольшее.

y(–4)=(–4+2)²·(–2+5)+2=4·3+2=14
y(–1/2)=((–1/2)+2)²·((–1/2)+5)+2=(9/4)·(9/2)+2=(81/8)+2 =10 целых 1/8
О т в е т. 14

13.
2sinx·cosx=sin2x

Разложим левую часть на множители способом группировки
(8sinx·cos³x–2sin2x)–(2cos²x–1)=0
(4·sin2x·cos²x–2sin2x)–(2cos²x–1)=0
2sin2x·(2cos²x–1)–(2cos²x–1)=0
(2cos²x–1)·(2sin2x–1)=0
2cos²x–1=0 или 2sin2x–1=0
cos²x=1/2
cosx=–√2/2 или сosx=√2/2 или sin2x=1/2

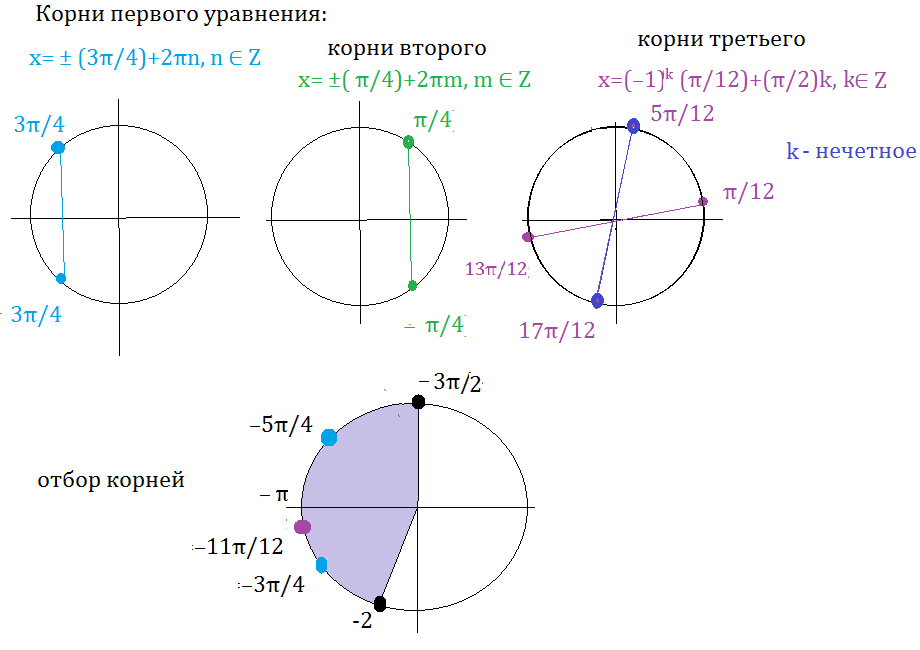
x= ± (3π/4)+2πn или x= ±( π/4)+2πm или x=(–1)^k(π/12)+(π/2)k,
n, m, k ∈ Z

Cм. приложение.

Указанному отрезку принадлежат корни
x=–5π/4
x=–11π/12
x=–3π/4