Задача 34342 ...
Условие
2) 4sin²2x+3=4cos²x
Решение
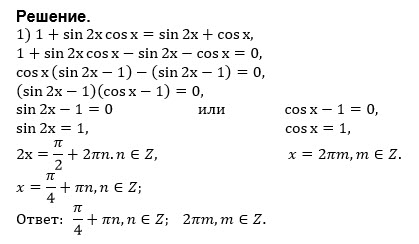

Все решения
sin2x(cosx -1) - (cosx -1) = 0
(cos x -1)(sin2x -1) = 0
cosx -1 = 0 sin2x -1 = 0
cosx = 1 sin2x = 1
x = πk, k ∈Z 2x =π/2 + πn, n ∈Z
x = π/4 + πn/2, n ∈Z
4sin²2x+3=4cos²x
4·4sin²x·cos²x+3-4cos²x=0
4cos²x(4sin²x-1)+3=0
4cos²x·(4sin²x-4+3)+3=0
4cos²x(3-4cos²x)+3=0
12cos²x-16cos⁴x+3=0
cos²x=t
t>0;t≤1;
16t²-12t-3=0
t₁,₂=[6⁺₋√(36+4·16·3)]/32=(6⁺₋√228)/32=(6⁺₋15.1)/32;
t₁=(6+15.1)/32=0.659;⇒cos²x=0.659;⇒cosx=⁺₋√659=⁺₋0.812;
x₁=⁺₋arccos(0.812)+2kπ;k∈Z;
x₂=⁺₋arccos(-0.812)+2kπ;k∈Z;
t₂=(6-15.1)-32=-0.284⇒t<0⇒решения нет
