Задача 34310 3*2^(cosx+3sqrt(1-sin^2x))+11*2^(2cosx)-34...

slava191

2019-03-09 12:37:33

3*2^(cosx+3sqrt(1-sin^2x))+11*2^(2cosx)-34 = 0, [-Pi/2; 5Pi/2]

sova

2019-03-09 13:05:34

★

1-sin^2x=cos^2x
sqrt(cos^2x)=|cosx|

3*2^(cosx+3|cosx|)+11*2^(2cosx)-34=0

Раскрываем знак модуля:
[b](1)[/b]
cosx ≥ 0 ⇒ |cosx|=cosx

cosx+3|cosx|=cosx+3cosx=4cosx

Получаем квадратное уравнение относительно 2^(2cosx)
Замена переменной:
2^(2cosx)=t;
t>0

3*t^2+11t-34=0
D=121- 4*3*(-34)=529

t_(1)=(-11-23)/6=-17/3 или t_(1)=(-11+23)/6=2

t_(1) < 0

Обратная замена
2^(2cosx)=2
2cosx=1
cosx=1/2

1/2 > 0
удовлетворяет условию [b](1)[/b] раскрытия модуля: cosx ≥ 0

x= ± arccos(1/2)+2πn, n ∈ Z
[b]x= ± (π/3)+2πn, n ∈ Z[/b]

[b](2)[/b]
[b](1)[/b]cosx < 0 ⇒ |cosx|= -cosx

cosx+3|cosx|=cosx-3cosx=-2cosx

Получаем уравнение относительно 2^(2cosx)
Замена переменной:
2^(2cosx)=t;
t>0
2^(-2cosx)=1/t

3/(t)+11t-34=0

11t^2-34t+3=0

D=34^2- 4*11*3=1156-132=1024=32^2

t_(1)=(34-32)/22=1/11 или t_(1)=(34+32)/22=3

Оба корня положительны

Обратная замена
2^(2cosx)=1/11 или 2^(2cosx)=3

2cosx=log_(2)(1/11) или 2cosx=log_(2)3

cosx=(1/2)log_(2)(1/11) или cosx=(1/2)log_(2)3


log_(2)3 >1
(1/2)log_(2)3>0,5>0

не удовлетворяет условию [b](2)[/b] раскрытия модуля : cosx < 0

(1/2)log_(2)(1/11) < 0


log_(2)(1/11)= - log_(2)11

log_(2)11 >log_(2)8=3

- log_(2)11 < -3

(-1/2) log_(2)11 < -3/2

Уравнение
cosx=(1/2)log_(2)(1/11)

не имеет решений в силу ограниченности косинуса
|cosx| ≤ 1

О т в е т. ± (π/3)+2πn, n ∈ Z

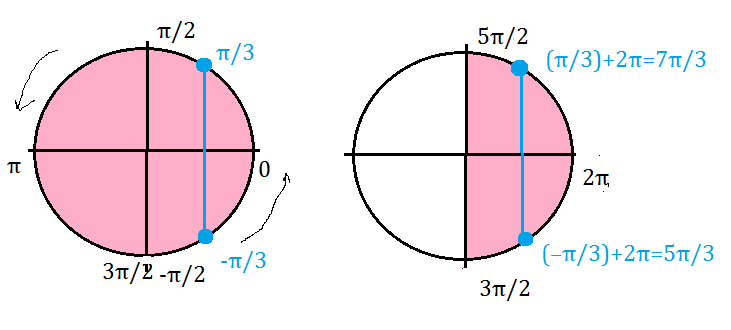
Отбор корней:

Указанному отрезку принадлежат корни:
(-π/3); (π/3); (-π/3)+2π=5π/3; (π/3)+2π=7π/3