Задача 34304 геометрическая задача 14...
Условие

Решение
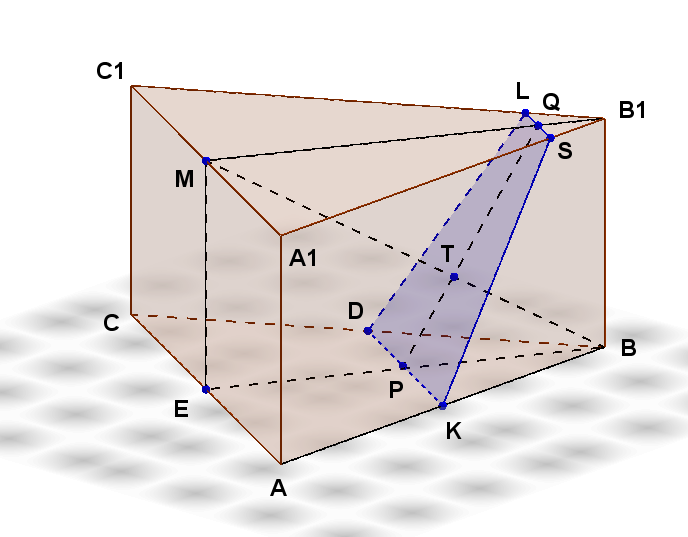
В правильной треугольной призме АВСА1В1С1 сторона основания АВ равна 6, а боковое ребро АА1 равно 3. На ребре В1С1 отмечена точка L так, что B1L=1. Точки К и М – середины ребер АВ и А1С1 соответственно. Плоскость у параллельна прямой АС и содержит точки К и L.
а) Докажите, что прямая ВМ перпендикулярна плоскости у
б) Найдите объем пирамиды, вершина которой – точка М, а основание – сечение данной призмы плоскостью у.
РЕШЕНИЕ:
а)Плоскости оснований призмы параллельны, поэтому сечение будет пересекать эти плоскости по прямым LS и DK, которые также параллельны. Пусть B1M — высота треугольника A1B1C1, а BE — высота треугольника ABC.
Из прямоугольного треугольника B1MA1 находим по теореме Пифагора B1M = 3·√3. Из прямоугольного треугольника B1QS находим по теореме Пифагора B1Q =√3/2. Тогда MQ = B1M – B1Q = (5·√3)/2.
Кроме того PB = (3·√3)/2 (половина высоты BE правильного треугольника ABC). Треугольники MQT и PTB подобны по двум углам (углы PTB и MTQ равны как вертикальные, углы TPB и MQT равны как накрест лежащие при параллельных прямых MQ, PB и секущей PQ). Их коэффициент подобия равен k =MQ/PB = 5/3.
Далее из прямоугольного треугольника MBE находим MB = √BE2+ME2 = 6. Используя доказанное подобие, находим TB = MB/(1+k) = 9/4. Аналогично, PQ = 2·√3. Следовательно, TP = 2√3/(1+k) = 3√3/4.
Проверяем, является ли треугольник TPB прямоугольным. Для этого используем теорему, обратную теореме Пифагора. TP2 = 27/16, TB2 = 81/16}, BP2 = 27/4. Получаем:
TP2+TB2=27/16+81/16=27/4=BP2.
Итак, треугольник TPB прямоугольный с прямым углом T. Доказано, что MB ⊥ PQ. По теореме о трёх перпендикулярах MB ⊥ DK . Получается, что MB перпендикулярен двум пересекающимся прямым, лежащим в плоскости DKS, а следовательно перпендикулярен этой плоскости.
б)Сечение DLSK — трапеция, площадь которой равна:
S=1/2·(LS+DK)·PQ=1/2·(1+3)·2√3=4√3.
Тогда объём искомой пирамиды равен:
V=1/3·S·MT=1/3·4√3·15/4=5√3.
ДАННЫЕ ПОДСТАВЬ СВОИ!!!!!