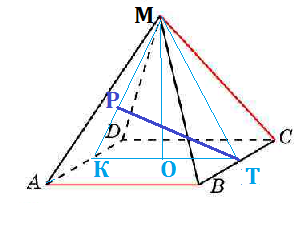
Задача 34296 48. В правильной четырехугольной...

vk160064007

8 марта 2019 г. в 16:56

48. В правильной четырехугольной пирамиде MACBD, все ребра которой равны 1, найдите расстояние между прямыми MA и ВС.

sova

8 марта 2019 г. в 17:20

★

BC||AD
MA и AD лежат в плоскости MAD.
Значит BC|| пл. MAD

Расстояние между прямой BA и пл. MAD – высота TP треугольника SKM.

Треугольник MKT – равнобедренный.
КT=AB=ВС=1
MK=MT=√3/2 – высоты равносторонних треугольников MAD и МBC со стороной 1.

MO – высота пирамиды

Из треугольника MOC
MO²=MC²–(OC)²=1–(√2/2)²=1/2
MO=√2/2

Применяем метод площадей
S( Δ MKT)=(1/2)KT·MO; S( Δ MKT)=(1/2)MK·TP ⇒

(1/2)KT·MO=(1/2)MK·TP

KT·MO=MK·TP

1·(√2/2)=(√3/2)·TP

TP=√2/√3=√6/3

О т в е т. √6/3