Задача 34286 Пусть прямая l1(4x–y+1=0) одна из...
Условие
Решение
Расстояние d от точки M(1;2) до прямой 4х-у+1=0
это длина стороны квадрата
d(M, 4x-y+1=0)=|4x_(M)-y_(M)+1|/sqrt(17)=|4*(1)-2+1|/sqrt(17)= [b]3/sqrt(17)[/b]
Уравнение прямой 4x-y+1=0 можно записать
y=4x+1
k=4
k=tg α ;
Значит прямая c угловым коэффициентом 4 - это диагональ прямоугольника, размеры 1 × 4 ( длина 1, высота 4: tgα=4/1)
Параллельная ей прямая проходит через точку М
k=4
y=4x+m
Чтобы найти m подставляем координаты точки M
2=4*1+m
m=-2
[b]y=4x-2[/b]
Перпендикулярная ей прямая имеет угловой k=-1/4
(потому что произведение угловых коэффициентов взаимно перпендикулярных прямых равно (-1))
y=(-1/4)x + b
Чтобы найти b подставляем координаты точки M
2=(-1/4)*1+b
b=2 целых 1/4
[b]y=(-1/4)x + 2 целых 1/4⇒ 4y+x-9=0[/b]
Третья сторона имеет угловой коэффициент k=(-1/4) и находится на расстоянии 3/sqrt(17) от точки M (1;2)
y=(-1/4)x+n
или
4y+x-4n=0
3/sqrt(17) =|4y_(M)+x_(M)-4n|/sqrt(17)
3/sqrt(17) =|4*1+2-4n|/sqrt(17)
|4*2+1-4n|=3 ⇒
9-4n=-3 или 9-4n=3
n=3 или n=3/2
[b]4y+x-12 =0[/b] или [b]4y+x-6=0[/b]
О т в е т. [b]y=4x-2[/b]; [b]4y+x-9=0[/b]; [b]4y+x-12 =0[/b] (или [b] 4y+x-6=0[/b])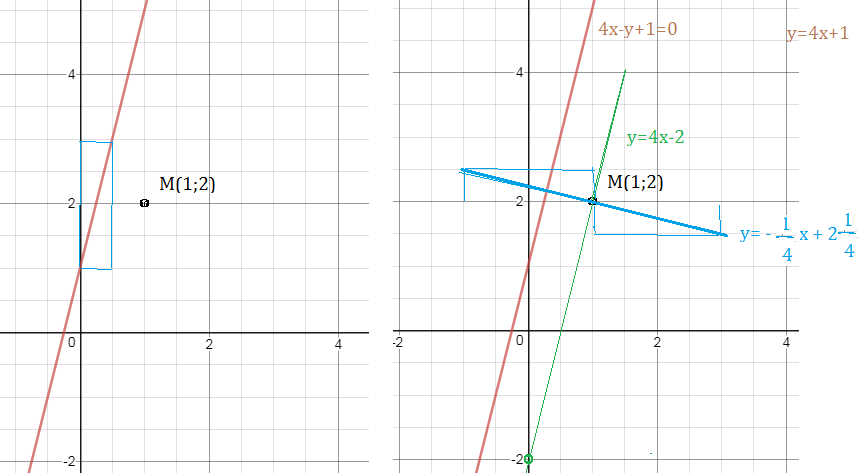
Все решения


