Задача 34205 ...

161616

2019-03-05 18:03:24

Задачи 1,3,5,7,пожалуйста)

Расстояние между скрещивающимися прямыми

1) Дано: А... D_1 — куб, площадь поверхности которого равна 96 см ². Найти: расстояние между прямыми АB₁ и DD₁.

3) Дано: А... D_1 — куб с ребром, равным √72 см. Найти: расстояние между прямыми А_1А и BD₁.

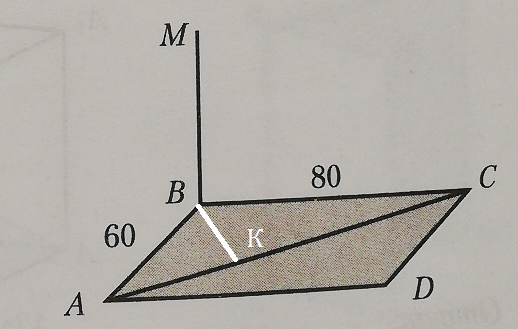
5) Дано: ABCD — прямоугольник, МB⊥ (ABCD), AB = 60, BC = 80. Найти: расстояние между прямыми MB и AC.

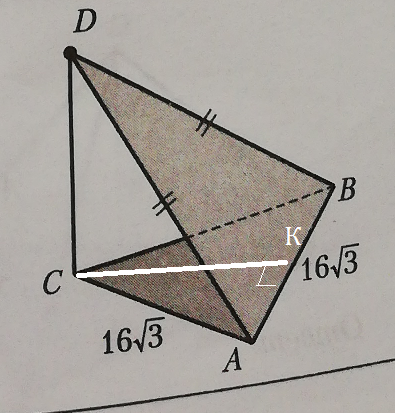
7) Дано: DC ⊥ (ABC), AC = AB = 16√3, AD = BD. Найти: расстояние между прямыми AB и DC.

sova

2019-03-05 18:19:46

★

1)
Пусть ребро куба равно a.
S_(поверхности куба)=6a^2

6a^2=96
a^2=16
a=4

ρ(AB_(1),DD_(1))=ρ(AB_(1), пл. DD_(1)C_(1)C)=AD=4

3)
ρ(AA_(1),BD_(1))=ρ(AA_(1), пл. BB_(1)D_(1)D)=(1/2)AC=6,

так как АС=sqrt(72)*sqrt(2)=sqrt(144)=12

5)
ρ(MB,AC)=BK,
BK ⊥ AC

AC=100 ( египетский треугольник, или по теореме Пифагора)
Согласно метода площадей:
ab/2=ch/2⇒

ВК=60*80/100=48

ρ(MB,AC)=48

7) AD=BD ⇒ равные наклонные имеют равные проекции
АС=ВС
АС=АВ=ВС=16sqrt(3)
Δ АВС - равносторонний

Проводим СК ⊥ АВ

СК=16sqrt(3)*sqrt(3)/2=24

ρ(CD,AB)=CK=24