Задача 34198 Решить логарифмическое уравнение: 1)...
Условие
1) log3(x-7) = 0
2) log2(x^2-3x+10) = 3
3) (1/2)lg(5x-4) + lgsqrt(x+1) = 2+lg0,18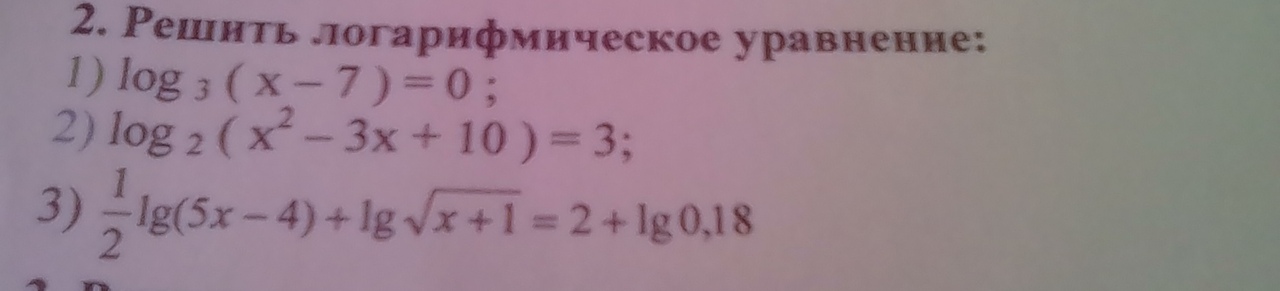
Решение
1) По определению логарифма
x-7=3^(0)
x-7=1
x=8
Проверка:
log_(3)(8-7)=log_(3)1=0 - верно
О т в е т. 8
2)
x^2-3x+10=2^3
x^2-3x+2=0
D=9-4*2=1
x_(1)=(3-1)/2=1; x_(2)=(3+1)/2=2.
Проверка:
x=1
log_(2)(1^2-3*1+10)=log_(2)8=3- верно
x=2
log_(2)(2^2-3*2+10)=log_(2)8=3- верно
О т в е т. 1; 2
3)
ОДЗ:
{5x-4 > 0 ⇒ x > 0,8
{x+1 > 0 ⇒ x > -1
ОДЗ: х > 0,8
lgsqrt(x+1)=lg(x+1)^(1/2)=(1/2)lg(x+1)
(1/2)lg(5x-4)+(1/2)lg(x+1)=lg100+lg0,18
Умножаем уравнение на 2
lg(5x-4)+lg(x+1)=2*(lg100+ lg0,18)
Сумму логарифмов заменим логарифмом произведения
lg(5x-4)*(x+1)=lg18^2
(5x-4)(x+1)=324
5x^2+x-328=0
D=1+20*328=6561=81^2
x_(1)=(-1-81)/10= - 8,2; x_(2)=(-1+81)/10=8
x_(1) не удовлетворяет ОДЗ
О т в е т. 8
