Задача 34166 16.4. Образующая конуса длиной 9 см...
Условие
16.7. Радиус основания цилиндра равен r, а радиус шара, описанного около этого цилиндра, равен R. Найдите площадь боковой поверхности цилиндра.
Решение
Значит осевое сечение конуса - равносторонний треугольник.
Требуется найти радиус окружности, описанной около этого равностороннего треугольника.
R=a*sqrt(3)/3
(Формула легко получается из условия, что О- точка пересечения биссектрис, медиан и высоты. Медианы в точке пересечения делятся в отношении 2:1,считая от вершины.
R=(2/3)h_(Δ)
h_(Δ)=a*sin60^(o)=asqrt(3)/2)
При a=9
R=9*sqrt(3)/3= [b]3sqrt(3)[/b].
О т в е т. 3sqrt(3)
16.7
Осевое сечение цилиндра - прямоугольник.
Прямоугольник вписан в окружность.
По теореме Пифагора
H^2=(2R)^2-(2r)^2=4*(R^2-r^2)
H=2sqrt(R^2-r^2)
S_(бок. цилиндра)=2π*r*H=2π*r*2sqrt(R^2-r^2)=4πr*sqrt(R^2-r^2)
О т в е т.4πr*sqrt(R^2-r^2) 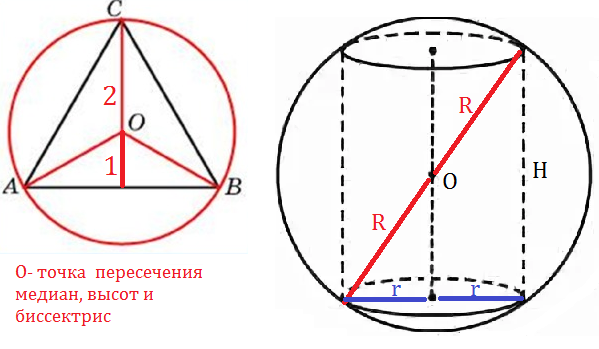
Все решения
В равностороннем треугольнике R=a/sqrt(3).
Ответ:3sqrt(3).
