Задача 34109 ...

mumiya

2019-03-02 18:46:02

Найти площадь фигуры, задаваемой на координатной плоскости соотношениями

5х+6у ≤ 7
у ≤ 2
(5х+4у+7)(5х-2у-11)=0
(все три строчки находятся под знаком системы)

sova

2019-03-02 20:02:21

★

Рисуем границу каждой области:
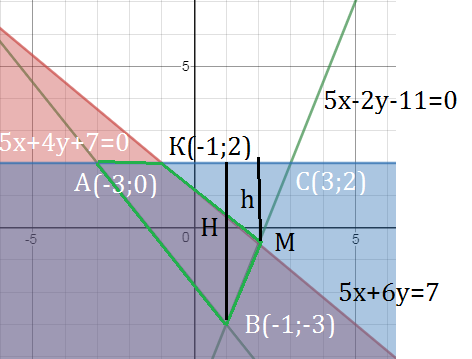
1)5х+6у=7 - прямая, проходящая через точки (5;-3) и (-1;2)
Область
5х+6у ≤ 7 содержит точку (0;0)
0+0 ≤ 7 - верно
2) y=2 - прямая || оси Ох
y ≤ 2 - область ниже прямой y=2
3)(5х+4у+7)(5х–2у–11)=0 - произведение равно 0 когда хотя бы один из множителей равен 0.
5х+4у+7=0 - прямая проходит через точки (-3;0) и (-1;-3)
5х–2у–11=0 - прямая проходит через точки (3;2) и (-1;-3)

Все три условия ограничивают четырёхугольник АКМВ
S_(AKMB)=S_( Δ ABC)-S_( Δ КСМ)

Надо найти координаты точки М, точки пересечения прямых
{5x+6y=7⇒ 5x=7 - 6y
{5x-2y-11=0 ⇒ 5x=2y+11
Приравниваем правые части
7-6у=2у+11
-8у=4
у=-1/2
Можно даже х не находить

S_(AKMB)=S_( Δ ABC)-S_( Δ КСМ)=

=(1/2)AC*H-(1/2)KC*h
H=5 ( 5 клеточек на рисунке)
h=2,5 ( ордината точки М найдена)

=(1/2)*6*5-(1/2)*4*2,5=15-5=10

О т в е т. 10