Задача 34089 system{(x-1)(y-1) = 1; x^2y+xy^2=16}...

slava191

2019-03-02 11:26:40

system{(x-1)(y-1) = 1; x^2y+xy^2=16}

sova

2019-03-02 16:12:28

★

Из первого уравнения
xy-y-x+1=1
xy=x+y

Подставляем во второе

(xy)^2=16
xy= - 4 или хy=4

Получаем совокупность двух систем
{x+y=-4
{xy= -4
или
{x+y=4
{xy=4

Решаем каждую способом подстановки

{y=-4-x
{x*(-4-x)=-4 ⇒ x^2+4x-4=0 ⇒ D =16+16=32
x_(1)=(-4-4sqrt(2))/2= -2-2sqrt(2); x_(2)=(-4+4sqrt(2)/2= -2+2sqrt(2);
y_(1)=- 4-x_(1)= -2+2sqrt(2); y_(2)=- 4-x_(2)=- 2-2sqrt(2)

{y=4-x
{x*(4-x)=4 ⇒ x^2-4x+4=0 ⇒ (x-2)^2=0 ⇒x_(3)=2
y_(3)=4-x_(3)=4-2=2

О т в е т. (2;2); (-2-2sqrt(2);-2+2sqrt(2)); (-2+2sqrt(2);-2-2sqrt(2))

Р.S
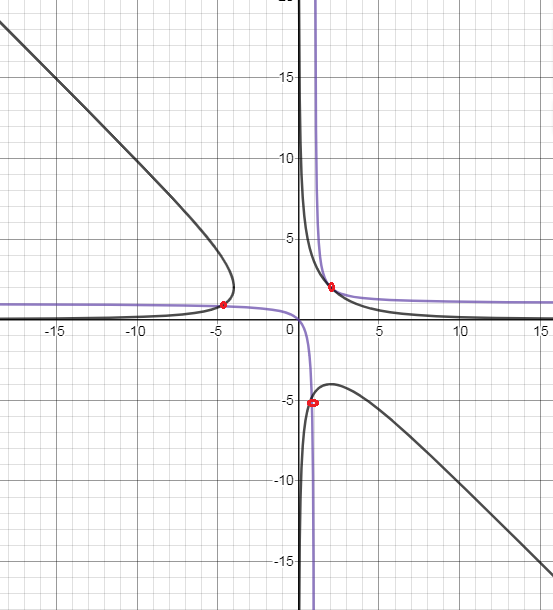
На рисунке графическое решение системы: