Задача 34053 ...
Условие
∫ (x^2+x+1)/((x+2)(x^2+2x+1)) dx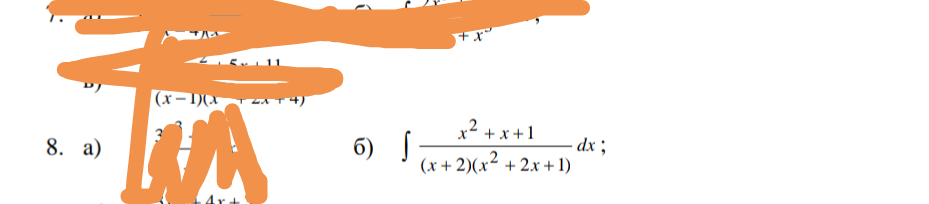
Все решения
∫ (x^2+x+1)dx/(x+2)(X+1)^2= ∫ 3dx/(x+2)- ∫ 2dx/(x+1)+ ∫ dx/(1+x)^2=
=3ln| x+2|-2ln|x+1|-1/(x+1)+c.
∫ (x^2+x+1)/((x+2)(x^2+2x+1)) dx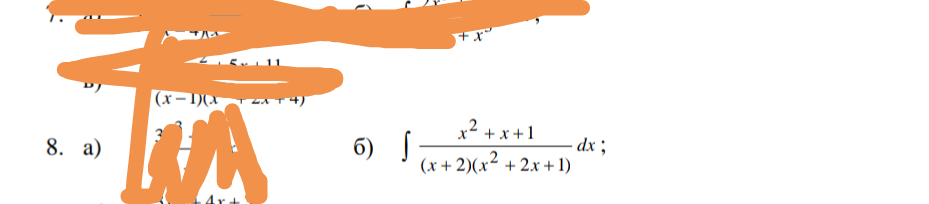
∫ (x^2+x+1)dx/(x+2)(X+1)^2= ∫ 3dx/(x+2)- ∫ 2dx/(x+1)+ ∫ dx/(1+x)^2=
=3ln| x+2|-2ln|x+1|-1/(x+1)+c.