Задача 34016 1. На рисунке 140, а изображена...

vk252862320

27 февраля 2019 г. в 20:28

1. На рисунке 140, а изображена четырехугольная пирамида SABCD. Точки К, Р и Т — середины ребер SD, AD и DC соответственно. Какое из утверждений является верным: ...

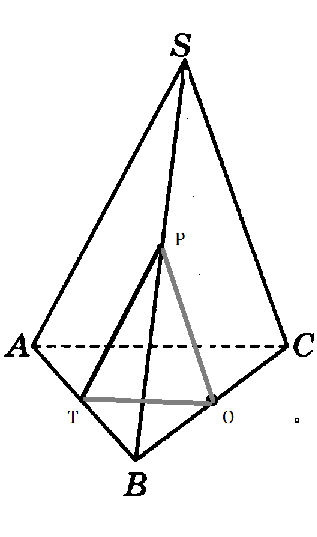
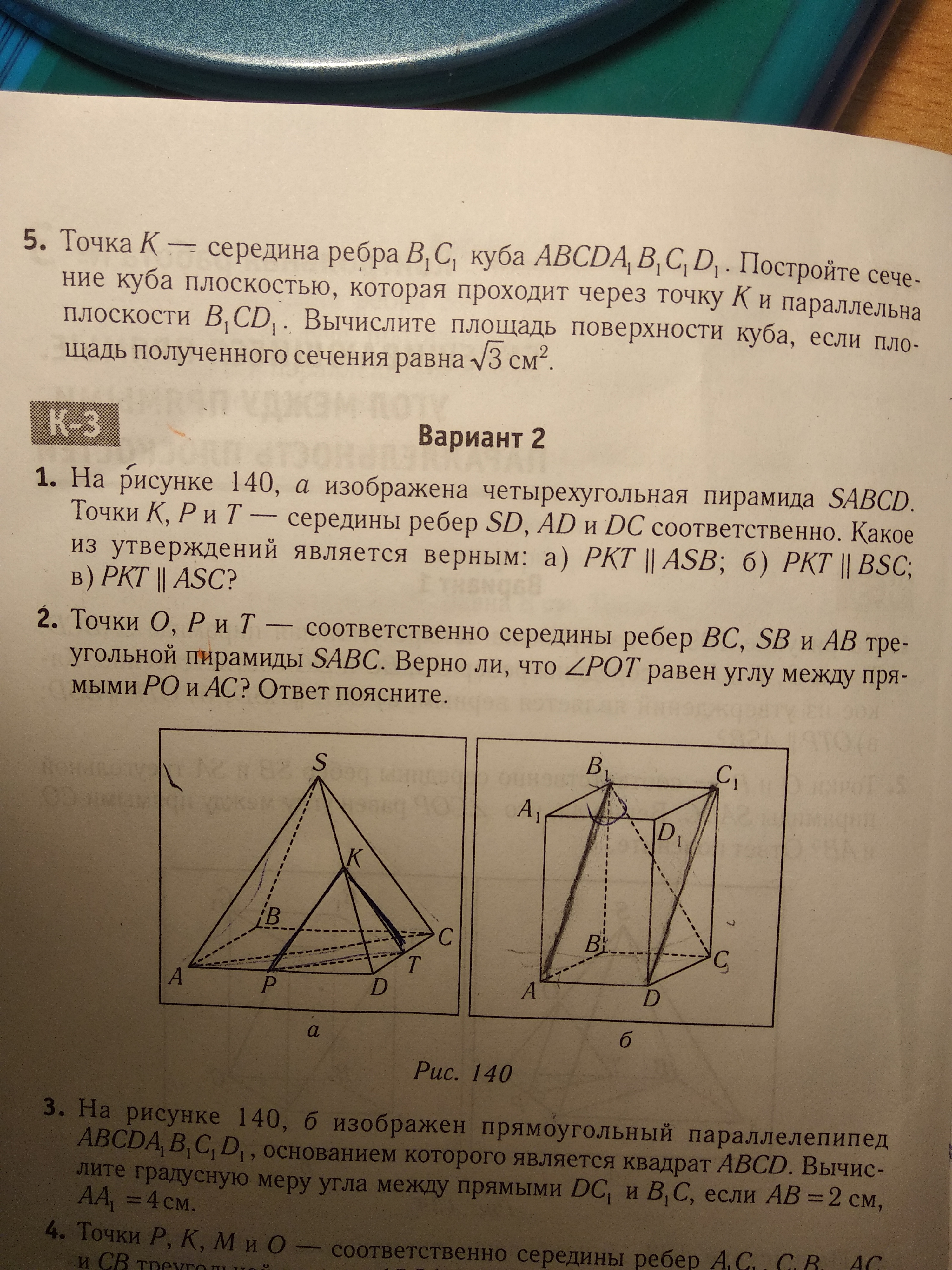
2. Точки О, Р и Т — соответственно середины ребер ВС, SB и АВ треугольной пирамиды SABC. Верно ли, что угол POT равен углу между прямыми РО и AC? Ответ поясните.

sova

27 февраля 2019 г. в 20:50

1.
PT– средняя линия Δ ADC
PT||AC
КТ – средняя линия Δ SCD
КТ|| SC
Две пересекающиеся прямые одной плоскости,
PT и КT параллельны двум пересекающимся прямым другой плоскости AC и SC
По признаку параллельности двух плоскостей, такие плоскости параллельны

верно в)
2.
Да, так как
ОТ|| AC

∠ POT – угол между PO и ОТ, а значит и между РО и АС