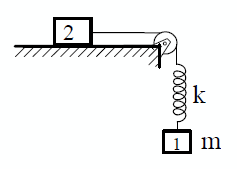
Груз массы m подвешен через пружину жёсткости k на нерастяжимой нити, перекинутой через блок, соединённой с бруском 2, лежащим на горизонтальной плоскости. В начальный момент груз m удерживается так, что пружина находится в ненапряжённом состоянии, затем его отпускают без начальной скорости. Найдите минимальную массу бруска 2, при которой он ещё будет оставаться неподвижным. Коэффициент трения между бруском 2 плоскостью равен µ. Массой пружины, нити, блока и трением в нём пренебречь.
физика 10-11 класс
12730
Брусок массы M на плоскости остается неподвижным до тех
пор, пока сила упругости, действующая на него со стороны нити, не
достигнет максимального значения силы трения покоя.

Ответ: M=2m/u
Вопросы к решению (1)
почему максимальное растяжение пружины в 2 раза больше амплитуды?

