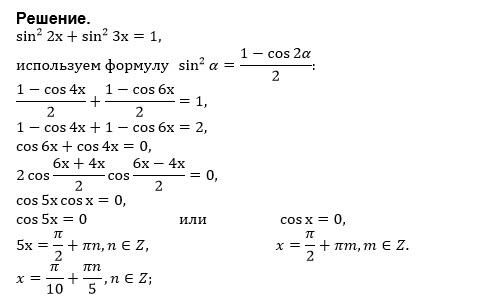Задача 33946 ...

vk331073901

2019-02-26 22:03:59

Найти сумму корней на отрезке

Sin² 2x + sin² 3x = 1, x ∈ [0; 2π]

sova

2019-02-26 22:41:49

★

(1-cos4x)/2 + (1-cos6x)/2=1;

-cos4x - cos6x=0
cos4x+cos6x=0

2cos5x*cosx=0

cos5x=0 ⇒ 5x=(π/2)+πn, n ∈ Z ⇒ x=(π/10)+(π/5)*n, n ∈ Z

cosx=0 ⇒ x=(π/2)+πk, k ∈ Z

Второй ответ включен в первый.

О т в е т. [b] (π/10)+(π/5)*n, n ∈ Z[/b]

Отрезку [0;2π] принадлежат 10 корней:

(π/10)
(π/10)+(π/5)=(3π/10)
(π/10)+(π/5)*2=(5π/10)=(π/2)
(π/10)+(π/5)*3=(7π/10)
(π/10)+(π/5)*4=(9π/10)
(π/10)+(π/5)*5=(11π/10)
(π/10)+(π/5)*6=(13π/10)
(π/10)+(π/5)*7=(15π/10)=(3π/2)
(π/10)+(π/5)*8=(17π/10)
(π/10)+(π/5)*9=(19π/10)

Сумма корней
S=(π/10)+(3π/10)+(5π/10)+(7π/10)+(9π/10)+(11π/10)+(13π/10)+(15π/10)+(17π/10)+(19π/10)=

=(π/10)*(1+3+5+7+9+11+13+15+17+19)= (π/10)*(1+19)*10/2=

= (π/10)*(100)=10π