Задача 33893 ...

sa2842004

2019-02-25 17:01:26

√(х-1) *(х-2)(х+1)<0
(Метод интег.)

sova

2019-02-25 17:05:31

ОДЗ:
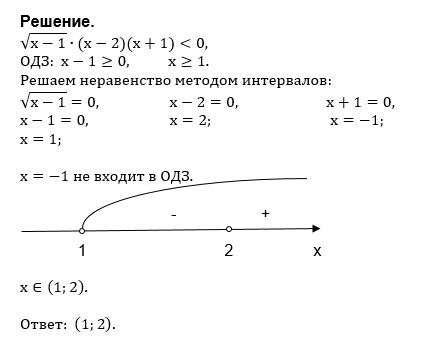
x-1 ≥ 0 ⇒ x ≥ 1

Решаем неравенство методом интервалов.

Находим нули функции
f(x)=sqrt(x-1)*(x-2)*(x+1)

sqrt(x-1)=0 ⇒ x = 1
или
x-2=0 ⇒ x = 2
или
x+1=0 ⇒ x = -1 не входит в ОДЗ

Расставляем знак функции на ОДЗ.

Неравенство строгое, нули функции отмечаем пустым кружком,
на рисунке круглые скобки:

(1) __-__ (2) __+__

На (2;+ ∞ ) ставим знак +,
так как в произвольной точке этого промежутка,
например в точке х=10
f(10)=sqrt(10-1)((10-2)*(10+1)>0

Далее знаки чередуются справа налево.

О т в е т. (1;2)