Задача 33857 ...
Условие
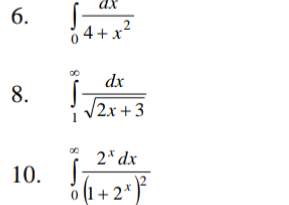
математика ВУЗ
1427
Все решения
∫ ^(+ ∞ )_(0)dx/(4+x^2)=lim_(A→+∞) ∫ ^(A)_(0)dx/(4+x^2)=
=lim_(A→+∞)(1/2)atctg(x/2)| ^(A)_(0)=
=(1/2)*lim_(A→+∞)atctg(A/2)-(1/2)arctg0=
=(1/2)*(π/2)=π/4
Сходится
8
∫ ^(+ ∞ )_(1)dx/sqrt(2x+3)=lim_(A→+∞) ∫ ^(A)_(0)dx/sqrt(2x+3)=
=lim_(A→+∞) (1/2) ∫ ^(A)_(0)d(2x+3)/sqrt(2x+3)=
=lim_(A→+∞)(1/2)* (2*sqrt(2x+3))| ^(A)_(1)=
=lim_(A→+∞) sqrt(2*A+3)- sqrt(5)=+ ∞
Расходится.
10
=lim_(A→+∞)(1/ln2)*(-1/(1+2^x))|^(A)_(0)=
=(1/ln2)(0+1)=1/ln2
Сходится
