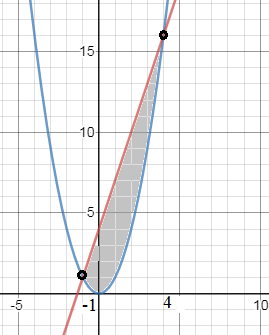
Задача 33856 Найти площадь фигуры,огранич.линиями...
Условие
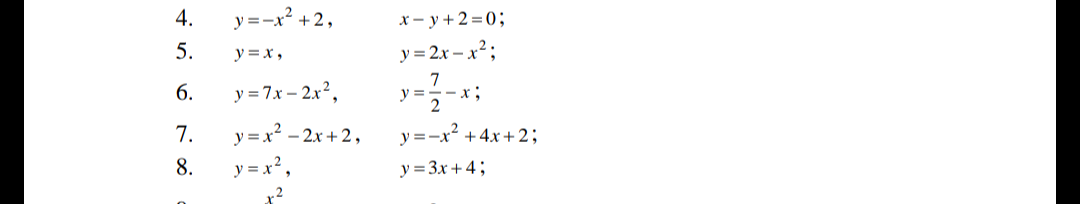
математика ВУЗ
879
Все решения
x^2-3x-4=0
D=9+16=25
х=(3-5)/2=-1 или х=(3+5).2=4
S= ∫ ^(4)_(1) ((3x+4)-x^2)dx=
=((3x^2/2)+(4x)- (x^3/3))|^(4)_(-1)=
=(3/2)*(4^2-(-1)^2) +4*(4-(-1))-(1/3)*(4^3-(-1)^3)=
=68 целых 5/6