Задача 33855 ...
Условие
∫ xdx/(sin^2x) от Pi/4 до Pi/3
∫ (4x-1)dx/sqrt(3x+2) от 0 до 2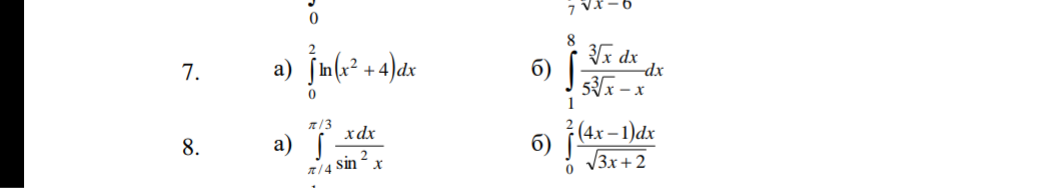
Все решения
u=x
dv=dx/sin^2x
du=dx
v=-ctgx
=(-x*ctgx)|^(π/3)_(π/4)- ∫ ^(π/3)_(π/4)(-ctgx)dx=
=-(π/3)*ctg(π/3)+(π/4)ctg(π/4) + ∫ ^(π/3)_(π/4)d(sinx)/sinx=
=(π/4)-(π*sqrt(3)/9) +ln|sinx||^(π/3)_(π/4)=
=(π/4)-(π*sqrt(3)/9) +ln|sin(π/3)|-ln|sin(π/4)|=
=(π/4)-(π*sqrt(3)/9) +ln(sqrt(3)/sqrt(2)).
8б
Замена
sqrt(3x+2)=t
3x+2=t^2
x=(t^2-2)/3
dx=2tdt/3
4x-1=4*(t^2-2)/3 - 1= (4t^2-11)/3
Меняем пределы интегрирования
x=0 ⇒ t=sqrt(3)
x=2 ⇒ t=sqrt(8)
получим
∫ ^(sqrt(8))_(sqrt(3))((4t^2-11)/3)*(2tdt/3)*(1/t)=
=(2/9)∫ ^(sqrt(8))_(sqrt(3))(4t^2-11)dt=
=(2/9)*(4t^3/3)|(sqrt(8))_(sqrt(3)- (22/9)(x)|^(sqrt(8))_(sqrt(3)=
=(8/17)(sqrt(8))^3-(8/17)(sqrt(3))^3-(22/9)*(sqrt(8)-sqrt(3))=
=(128sqrt(2))/17 - (24sqrt(3)/17)-(44sqrt(2)/9) +(22sqrt(3)/9)
можно привести подобные 1 и 3, 2 и 4
