Задача 33837 Дано уравнение 2sin2xsin(5Pi/2 - x) -...

opppai

23 февраля 2019 г. в 15:20

Дано уравнение 2sin2xsin(5π/2 – x) – √3sin2x + cos2x – √3cosx + 1 =0

a) Решите уравнение

б) Найдите все корни на промежутке [0;4]

sova

23 февраля 2019 г. в 16:16

Тема. Решение тригонометрических уравнений. Отбор корней.

По формулам приведения
sin((5π/2)–x)=cosx
По формулам двойного аргумента
cos2x=cos²x–sin²x=2cos²x–1
тогда уравнение примет вид:
2sin2x·cosx –√3·sin2x +2cos²x–1 – √3cosx+1=0
sin2x(2cosx–√3)+cosx·(2cosx–√3)=0
(2cosx–√3)·(sin2x+cosx)=0
2cosx–√3=0 или sin2x+cosx=0

(1) уравнение
2cosx–√3=0
cosx=√3/2
x= ± (π/6)+2πn, n ∈ Z

(2) уравнение
sin2x+cosx=0
2sinx·cosx+cosx=0
cosx=0 или 2sinx+1=0

cosx=0
x= (π/2)+πm, m ∈ Z

2sinx+1=0
sinx=–1/2
x=(–1)^k·(–π/6)+πk, k ∈ Z

Ответы ± (π/6)+2πn, n ∈ Z и (–1)^k·(–π/6)+πk, k ∈ Z
имеют пересечение в точке
– (π/6)+2πn, поэтому можно включить в ответ только один раз

О т в е т:
а)± (π/6)+2πn, (π/2)+πm, (–5π/6)+2πk, n , m, k ∈ Z
или
так:
а)(π/6)+πn, (–π/6)+2πk, (π/2)+πm, n , k, m ∈ Z

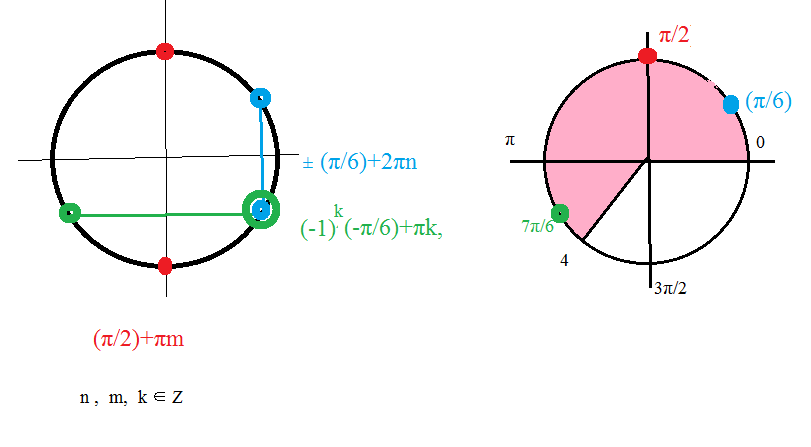
б)
(π/6);(π/2) и (7π/6) принадлежат отрезку [0;4]