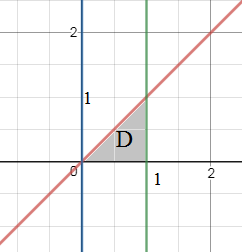Задача 33831 8) Найти наибольшее и наименьшее...
Условие

Решение
z`_(y)=-2xy+2y
Находим стационарные точки
{z`x=0
{z`y=0
{6x^2-y^2+10x=0
{-2xy+2y=0
{6x^2-y^2+10x=0
{2y*(-x+1)=0 ⇒ y=0; x=1
При y=0
6x^2-10x=0
x=0; x=5/3
При х=1
y^2=16
y= ± 4
Ни одна из них не является внутренней точкой области D.
Исследуем функцию на границе:
при[b]y=x[/b]
z=2x^3-x^3+6x^2
z=x^3+6x^2
Это функция одной переменной, исследуем ее как обычную параболу
при 0 ≤ x ≤ 1
Если х=0; y=0
z(0;0)=0
z=x^3+6x^2 возрастает на [0;1]
При x=1; y=1
z(1;1)=2-1+5+1=7
при [b]y=0[/b]
z=2x^3+5x^2 – как функция одной переменной на [0;1], эта функция принимает наибольшее значение при х=1,
наименьшее при х=0,
Если x=0; y=0
z=(0;0)=0
Если x=1;y=0
z=2*1–0+5*1+0 = 7
z(1;0)=7
При [b]x=0[/b]
z=y^2 – как функция одной переменной 0 ≤ y ≤ 1
Эта функция принимает наименьшее при y=0,
наибольшее значение при y=1:
z(0;0)=0
z(0;1)=0-0+0+1=1
При [b]x=1[/b]
z=2-y^2+5 +y^2
z=7
Эта функция принимает постоянное значение,
наибольшее значение при y=1:
z(1;0)=7
z(1;1)=7
О т в е т.
Наибольшее значение функции в области D равно 7; наименьшее равно 0.