Задача 33742 ...
Условие
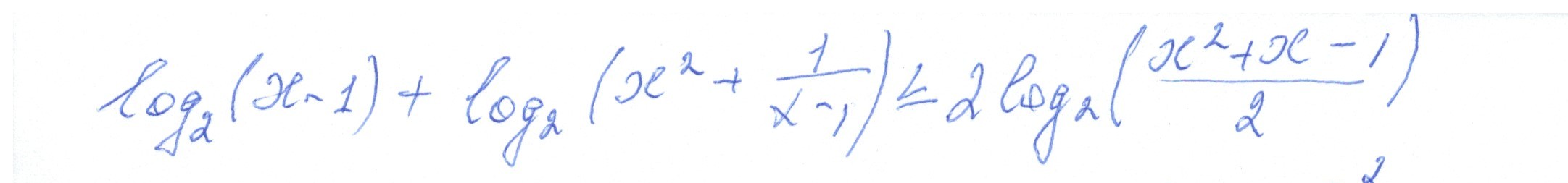
математика 10-11 класс
429
Все решения
Во втором логарифме нет x2 есть x + (1/(x–1))
Проверьте условие .
Решать то, что написано от руки – терять время.
Нужно прикреплять фото задания.
ОДЗ:
{x–1>0 ⇒ x>1
{(x2+x–1)/2>0 ⇒ x2+x–1 > 0 ⇒ D=5 ; x < (–1–√5)/2 или
x> (–1+√5)/2
(–1+√5)/2 < 1 ⇒ ОДЗ: (1;+ ∞ )
Применяем свойства логарифмов.
Заменим сумму логарифмов логарифмом произведения
log2(x–1)·(x+(1/(x–1)) ≤ 2·(log2((x2+x–1)/2)
(1/2)log2(x2–x+1) ≤ log2((x2+x–1)/2)
log2 √x2–x+1≤ log2((x2+x–1)/2)
Логарифмическая функция с основанием 2 возрастающая, поэтому
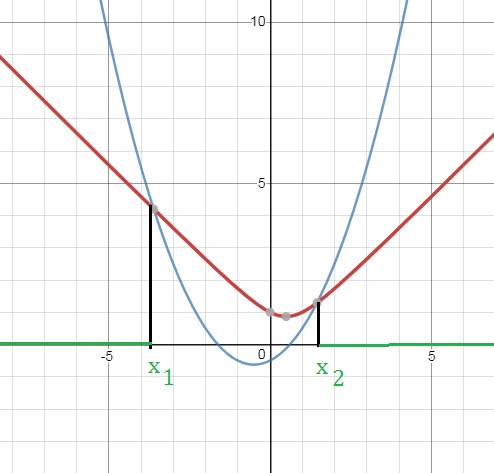
√x2–x+1≤ (x2+x–1)/2
x2–x+1 ≥ 0 при любом х.
D=1–4 <0
Обсуждения
