Задача 33706 [m] p_{\xi}(x) = \begin{cases} 0, & x <...

lizabeth

19 февраля 2019 г. в 10:29

[m] p_{\xi}(x) = \begin{cases}
0, & x < 0, \\
A \cdot x \cdot e^{-x}, & x \geq 0.
\end{cases} [/m]

a. значение константы A;

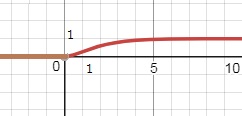
b. функцию распределения F_{\xi}(x) и построить ее график

sova

19 февраля 2019 г. в 13:28

★

По определению:
F_ξ(x)= ∫ ^x _{– ∞} p_ξ(x)dx
A=1 найдено ранее

Так как функция задана двумя выражениями рассматриваем
два случая:
при x < 0

F_ξ(x)=∫ ^x _{– ∞} 0(x)dx=0

При x ≥0

F_ξ(x)= ∫ ^x ₀x·e^–xdx=
считаем по частям
u=x
dv=e^–xdx
du=dx
v=–e^–x

=x·(–e^–x)|(х)₀ – ∫^х₀(–e^–x)dx

=–x·e^–x+0 – e^–x|^x₀=–x·e^–x–e^–x+1

Cм. рис.