Задача 33680 ...
Условие
и Р — середины рёбер AA₁ и BB₁ соответственно. Верно ли, что пря-
мые АР и ВР, (Параллельны плоскости ОС₁? Ответ обоснуйте.
4. Трапеция АВСО (АВ и CO), и квадрат АКМВ не лежат одной плоск
тановинами; все середины отрезков МО и КМ соответственно. Ус
тановимые прямых КO и MO.
Все решения
OB ∈ пл. В_(1)ОС_(1)
AP||OP
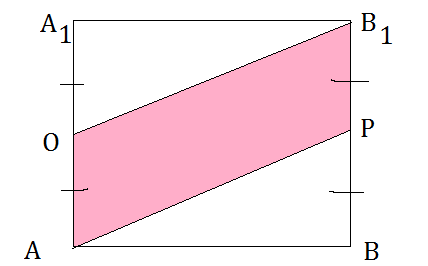
cм. рис.
ОВ_(1)РА - параллелограмм.
АО=(1/2)АА_(1)
B_(1)P=(1/2)BB_(1)
AA_(1)=BB_(1)
АО=B_(1)P
AA_(1)||BB_(1)
значит AO|| B_(1)P
Противоположные стороны четырехугольника равны и ||
Значит это параллелограмм
4.KD и OF - скрещивающиеся прямые,
так как три точки АОF лежат в одной плоскости, точка D так же принадлежит этой плоскости, потому как лежит на АО.
OF лежит в плоскости, а KD пересекает плоскость в точке, не принадлежащей OF