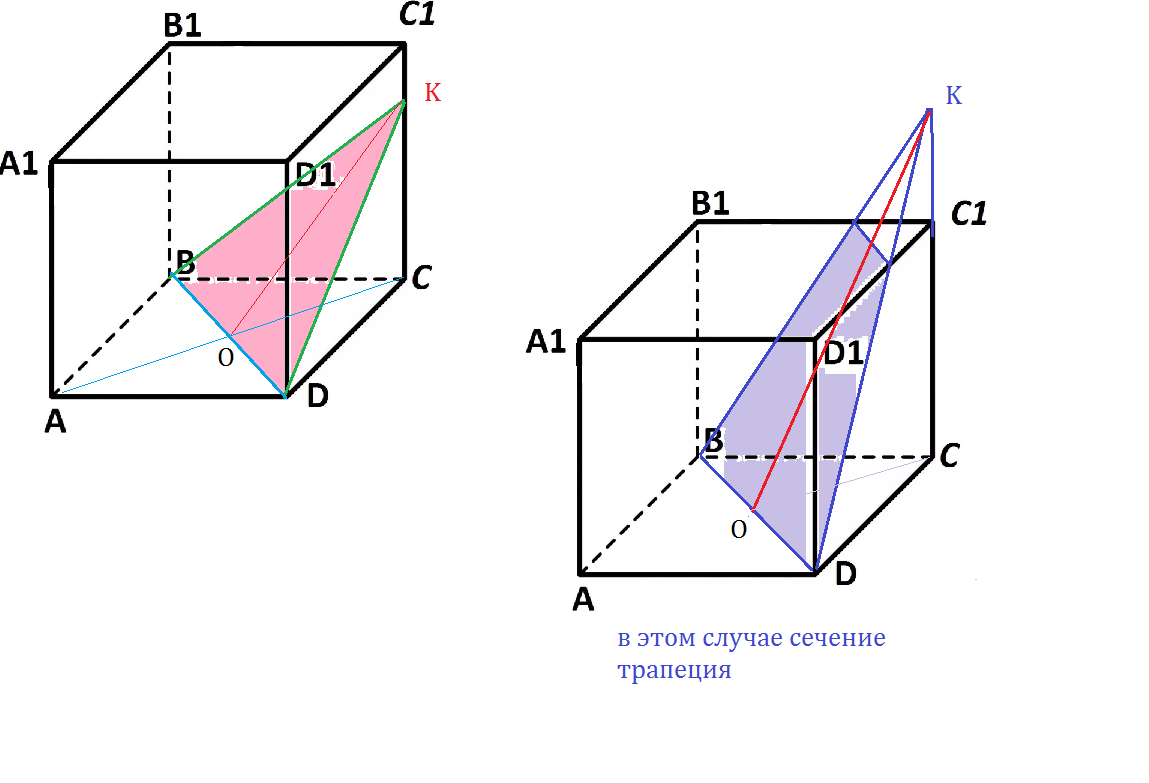
Задача 33655 Через диагональ грани куба построить...
Условие
Решение
S (грани)=a^2
Проведем сечение через диагональ BD.
BD=asqrt(2) - диагональ квадрата со стороной а
S_(cечения)=(1/2)*BD*h
(1/2)BD*h=a^2
(1/2)*asqrt(2)*h=a^2
h=asqrt(2)
Значит, ОК=h=asqrt(2)
Наибольшее значение, которое может принимать ОК
это положение OC_(1)
OC_(1)=sqrt(ОC^2+CC^2_(1))=sqrt((asqrt(2)/2)^2+a^2)=asqrt(3/2) < asqrt(2)
Значит, точка К расположена за точкой С_(1)
СK=asqrt(2)=2*OC
В этом случае в сечении трапеция и ее площадь меньше площади
треугольника BDK
ВЫВОД:
Значит, через диагональ грани можно провести сечение, равновеликое площади грани.
При этом высота треугольника BDK должна быть больше asqrt(2)
OC > asqrt(2)
[b]Основное решение[/b]:
В сечении равнобедренная трапеция.
Нижнее основание трапеции диагональ BD=asqrt(2)
Верхнее основание трапеции равно (a*sqrt(2))*k
k- коэффициент подобия
S_(трапеции)=(1/2)*(asqrt(2)+(asqrt(2))*k)H_(трапеции)
S_(трапеции)=S_(квадрата)=a^2
(1/2)a*sqrt(2)*(1+k)*H=a^2
[b](1+k)*H=asqrt(2)[/b] (#)
По теореме Пифагора
H^2=a^2+((1/2)asqrt(2)-(1/2)asqrt(2)*k)^2
H^2=a^2+(a^2/2)*(1-k)^2
Возводим равенство (#) в квадрат и подставляем H^2
(1+k)^2*(a^2+(a^2/2)*(1-k)^2)=2a^2
(1+k)^2*(2a^2+a^2-2a^2k+a^2k^2)=4a^2
(1+2k+k^2)*(3-2k+k^2)=4
4k^4+4k-1=0
Найдем k
k≈ 1/4