Задача 33617 7.43. Найдите 4x0^2, где x0 - наибольший...
Условие
[block](2x)/(x+1) + (1)/(x-1) - (4)/(x^2-4) = 0[/block]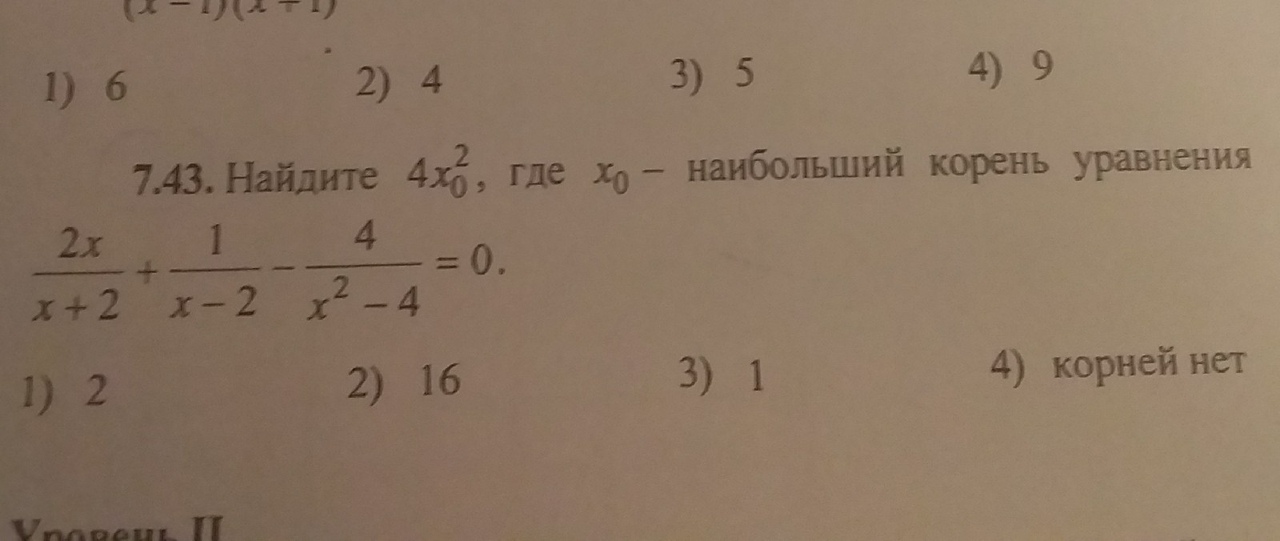
математика 10-11 класс
898
Решение
★
x^2-4=(x-2)(x=2):
(2x*(x-2)+(x+2)-4)/((x-2)(x+2))= 0
(2x^2-4x+x+2-4)/((x-2)(x+2)) = 0
(2x^2-3x-2)/((x-2)(x+4)) = 0
Дробь равна нулю тогда и только тогда, когда числитель равен нулю, а знаменатель отличен от нуля.
{2x^2-3x-2=0 ⇒D=9+16=25; x=(3-5)/4;[b] x=-1/2[/b]или x=(3+5)/4;[b]x=2[/b]
{(x-2)(x+2)≠ 0 ⇒ x ≠ 2 и x ≠ -2
Значит уравнение имеет единственный корень
х=-1/2
Обозначим
х_(o)=-1/2
тогда
4х^2_(o)=4*(-1/2)^2=4*(1/4)=1
О т в е т. 3)1