Задача 33494 1. На рисунке 30, а изображена...

vk261262348

12 февраля 2019 г. в 14:51

1. На рисунке 30, а изображена треугольная призма ABCA1B1C1, точка P — середина ребра AB, точка О — точка пересечения диагоналей грани AA1C1C, точка T — середина отрезка PC. Назовите боковую грань, плоскости которой параллельна прямая OT.

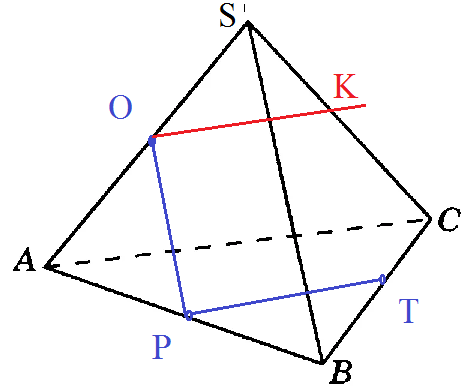
2. Точки O, P и T — соответственно середины ребер AS, AB и BC треугольной пирамиды SABC. Прямая / проходит через точку О и параллельна прямой AC. Установите взаимное расположение прямой / и плоскости SPT.

3. На рисунке 30, б, в изображена правильная пирамида SABCD. Точка Е лежит на ребре SB и SE: BE = 2:1, точка K — точка пересечения медиан грани DSC, а точка Pk — середина ребра DC. Докажите, что EK || ABC.

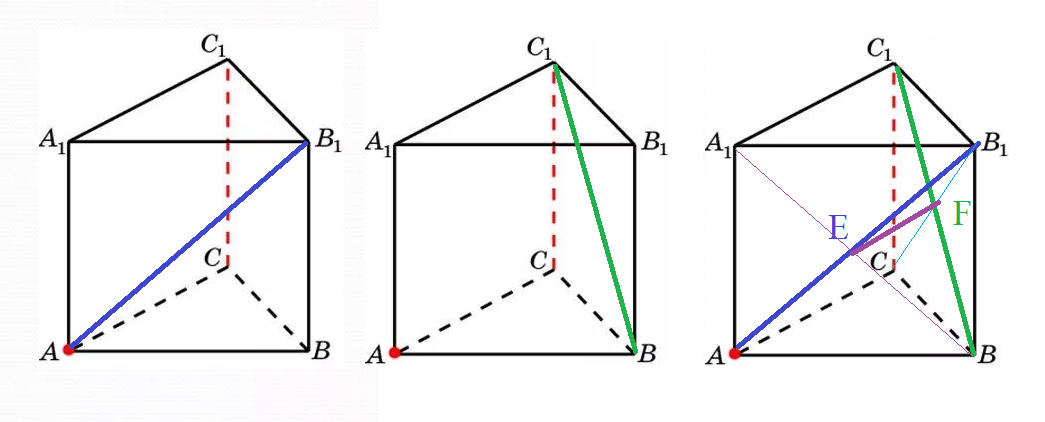
4. Длина каждого ребра прямой треугольной призмы ABCAB1C1 равна 8 см. Точки Е и F — середины отрезков В1А и ВС1 соответственно. Вычислите периметр треугольника BEF.

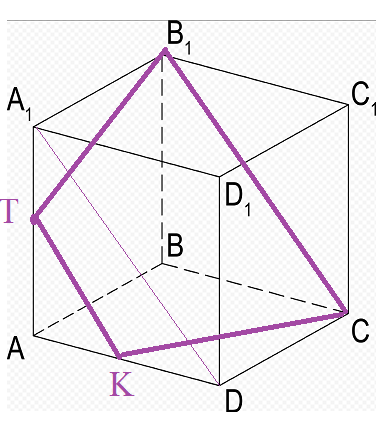
5. Точка T — середина ребра АА1 куба ABCDA1B1C1D1, длина ребра которого равна 6 см. Постройте сечение куба плоскостью В1СТ и вычислите его периметр.

sova

12 февраля 2019 г. в 17:51

1.

OT– средняя линия треугольника АРС
OT|| AP ⇒ OT || AA₁B₁B

2.
прямая l параллельна плоскости SPT
так как
PT– средняя линия Δ АВС
PT|| AC

прямая l пересекает OK ребро SC в точке К

OK || AC

Значит по свойству транзитивности
OK || PT ⇒ OK || пл. SPT

см. рис.

3.

В Δ SDC медиана SP соединяет вершину S c серединой противоположной стороны DC точкой P
K– точка пересечения медиан Δ SDC
Медианы в точке пересечения делятся в отношении 2:1, считая от вершины.
SK:KP=2:1

Треугольники SEK и SBP подобны, так как угол общий и стороны пропорциональны.

Значит EK || BP ⇒ EK || ABCD в том числе и АВС.

4.

См. приложение 2

диагонали боковой грани AA₁B₁B
A₁B и AB₁
пересекаются в точке E

A₁B=AB₁=8 √2 ( диагональ квадрата со стороной 8)

диагонали боковой грани СС₁B₁B
С₁B и СB₁
пересекаются в точке F

C₁B=CB₁=8 √2 ( диагональ квадрата со стороной 8)

Диагонали квадрата в точке пересечения делятся пополам
BE=BF=4 √2

EF– средняя линия Δ BA₁C₁

EF=(1/2)A₁C₁=4

P( Δ BEF)= BE+EF+FB=4√2+4+4√2=4+8√2

5.
Соединяем точки В₁ и С; В₁ и Т.
B₁C=6·√2 ( диагональ квадрата со стороной 6)
В₁Т=√6²+3²=√36+9=√45=3√5

Секущая плоскость пересекает параллельные плоскости по параллельным прямым.

Поэтому проводим
ТК || B₁ C || A₁D
A₁D=B₁C=6√2

ТK=(1/2)A₁D=3√2

KC=√KD²+DC²=3√5

Р (КТВ₁С)=КТ+ТВ₁+В₁С+СК=3√2+3√5+6√2+3√5=
=9√2+6√5