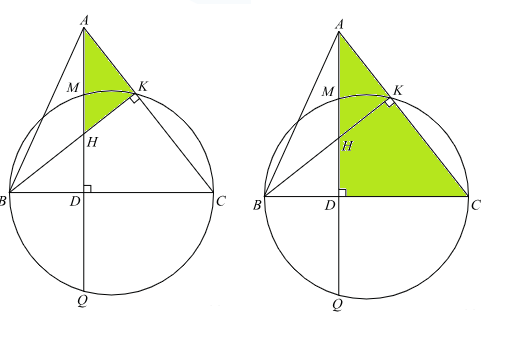
Задача 33490 на стороне BC остроугольного...

vk315458183

2019-02-12 13:18:58

на стороне BC остроугольного треугольника ABC как на диаметре построена полуокружность , пересекающая высоту AD в точке M, AD=9, MD=6, H-точка пересечения высот треугольникаABC. найдите AH

sova

2019-02-12 14:01:17

Продолжаем высоту AD за точку D до пересечения с окружностью в точке Q
MD=DQ=6
AM=AD-MD=9-6=3

По свойству секущих
AM*MQ=AK*AC
Так как
AM*MQ=3*(6+6)=36
Значит
АК*АС=36

Из подобия прямоугольных треугольников
АHК и АDC ( ∠ A - общий)
AH : AC = AK : AD

AH*AD=AC*AK
AH * 9 = 36
AH=4