Задача 33486 ...
Условие
Решение

Все решения
и
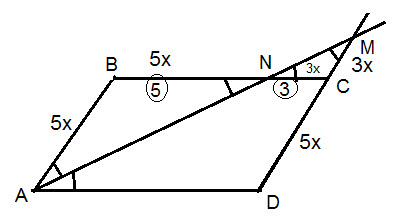
∠ NAD= ∠ ANB - внутренние накрест лежащие углы
⇒
∠ ВАN= ∠ ANB
Δ ABN - равнобедренный
Значит,
AB=BN
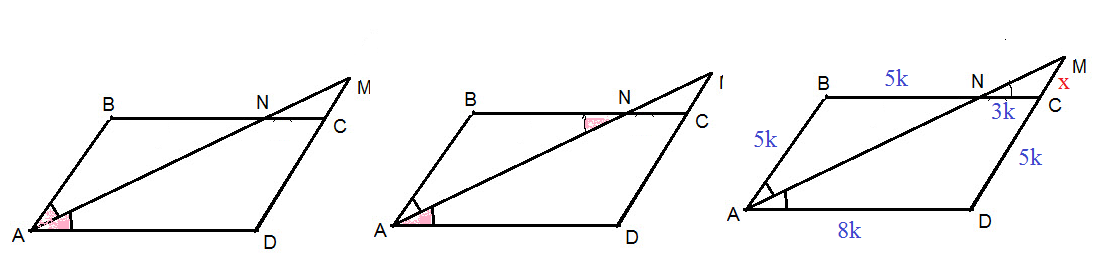
Обозначим k - коэффициент пропорциональности.
Тогда
BN=5k
NC=3k
BN:NC=5k:3k=5:3
AB=BN=5k
BC=BN+NC=5k+3k=8k
P=2*(AB+BC)=2*(5k+8k)=26k
26k=70
k=70/26=35/13
Треугольники MNC и MAD подобны ( NC || AD)
NC:AD=MC:MD
Пусть MC=x, тогда MD=MC+CD=x+5k
3k:8k=x:(x+5k)
8x=3*(x+5k)
8x=3x+15k
5x=15k
x=3k
x=3*(35/13)
MD=(x+5k)=8k=8*(35/13)=280/13
P.S
Если бы в задаче P было кратным 13-ти, тогда ответ - целое число