Задача 33484 ...

starrkz

2019-02-12 09:16:47

Найти (с точностью до сотых) площадь фигуры, ограниченной графиками решения уравнения:
​​(x-√(1-y^2))*(xy+y-x-1)*(y+1-x)=0

sova

2019-02-12 09:31:11

★

Произведение трех множителей равно 0 когда хотя бы один из них равен 0, [b] а другой при этом не теряет смысла [/b]

x-sqrt(1-y^2)=0 ⇒ x= sqrt(1-y^2) правая полуокружность
окружности
x^2+y^2=1
с центром (0;0) радиусом r=1

xy+y-x-1=0 ⇒ y(x+1)-(x+1)=0 ⇒ (x+1)*(y-1)=0 ⇒
Две прямые x=-1 или y=1


y+1-x=0 ⇒ y=x-1 - прямая.

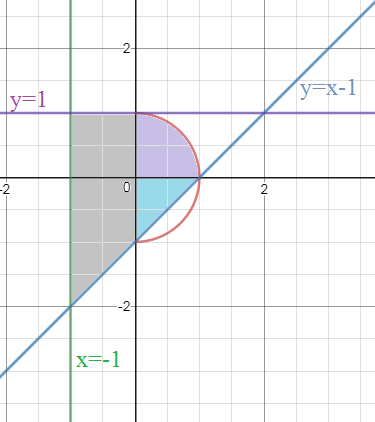
Строим фигуру.

S_(фигуры)=S_(трапеции)+(1/2)*S_(полукруга)+S_(Δ)

S_(трапеции)=(a+b)*h/2=(2+3)*1/2=5/2

(1/2)*S_(полукруга)=(1/4)π

S_( Δ)=(1/2)*1*1

О т в е т. (5/2)+(1/4)π+(1/2)=3+(π/4) ≈ 3+0,79=3,79