Задача 33381 Преобразование графиков функций. 5...
Условие
Построить график:
...
1) область определения функции;
2) область значения функции;
3) точки пересечения с осями координат;
4) промежутки возрастания функции;
5) промежутки убывания функции;
6) значения x, при которых f(x) > 0 и f(x) < 0;
Решение
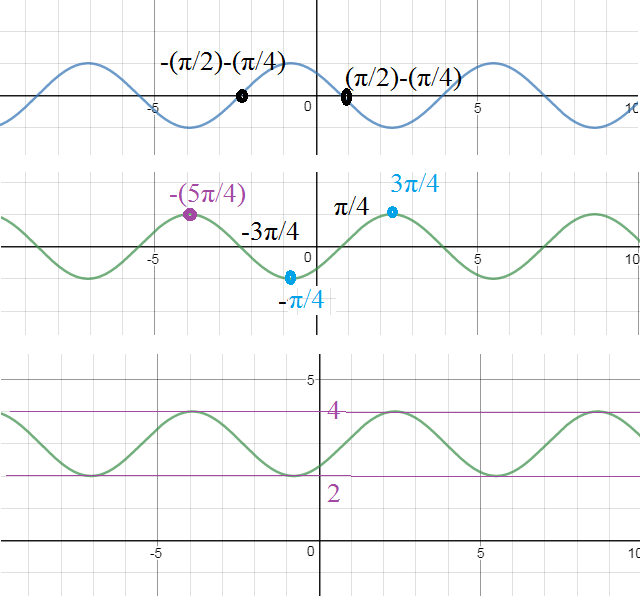
[b]y=3-cos(x+(π/4))[/b]
cм.приложение 1
1) используем известный график у= сosx
(его нет на рисунке)
2) строим y = cos(x + (π/4)) c помощью сдвига первого графика на
(π/4) влево см. рис.1
3) строим y= - cos(x+(π/4)) - зеркальное отражение графика 2)
см. рис.2
4) y=3-cos(x+(π/4) - параллельный перенос графика 3) на 3 единицы вверх см. рис. 3
область определения (- ∞ ;+ ∞ )
так как
-1 ≤ cosx ≤ 1 ⇒ -1 ≤ cos(x+(π/4)) ≤ -1 ⇒ -1 ≤ -cos(x+(π/4)) ≤ 1 ⇒
3-1 ≤ 3-cos(x+(π/4)) ≤ 3+1;
2 ≤ 3-cos(x+(π/4)) ≤ 4
область изменения [2;4]
точки пересечения с осями координат.
с осью Ох нет точек пересечения, график расположен выше оси Ох
с осью Оу
x=0; y=3-cos(π/4)=3-(sqrt(2)/2)
функция y = -cos x возрастает на (0+2πn, π+2πn), n ∈ Z
поэтому
данная функция возрастает на ((-π/4)+2πn, (3π/4)+2πn), n ∈ Z
функция y = -cos x убывает на (-π+2πn, 0+2πn), n ∈ Z
поэтому
функция убывает на ((-5π/4)+2πn; (-π/4)+2πn), n ∈ Z
f(x) > 0 при любом х
б)
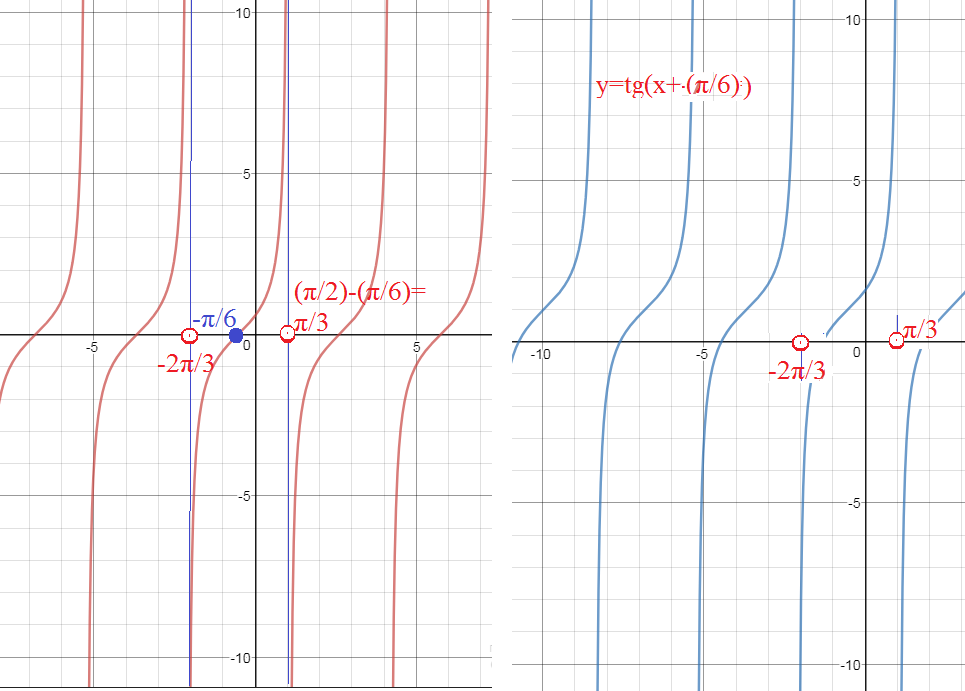
[b]y=tg(x+(π/6))[/b]
см. приложение 2
y=tg(x+(π/6)) получен из y=tgx сдвигом влево на (π/6)
соответственно точка (0;0) перемещается в точку (-π/6;0)
прямые х=(-π/2) и x=(π/2) - вертикальные асимптоты графика
y=tgx
в прямые
x=(- π/2)-(π/6)=-2π/3
и
y=(π/2) -(π/6)=π/3
Поэтому область определения данной функции
((-2π/3)+πn; (π/3)+πn), n ∈ Z
Область изменения (- ∞ ; +∞ )
Функция возрастает на каждом из интервалов
((-2π/3)+πn; (π/3)+πn), n ∈ Z
График y=tg(x+(π/6))+1 получен из y=tg(x+(π/6)) сдвигом на 1 единицу вверх.
в)
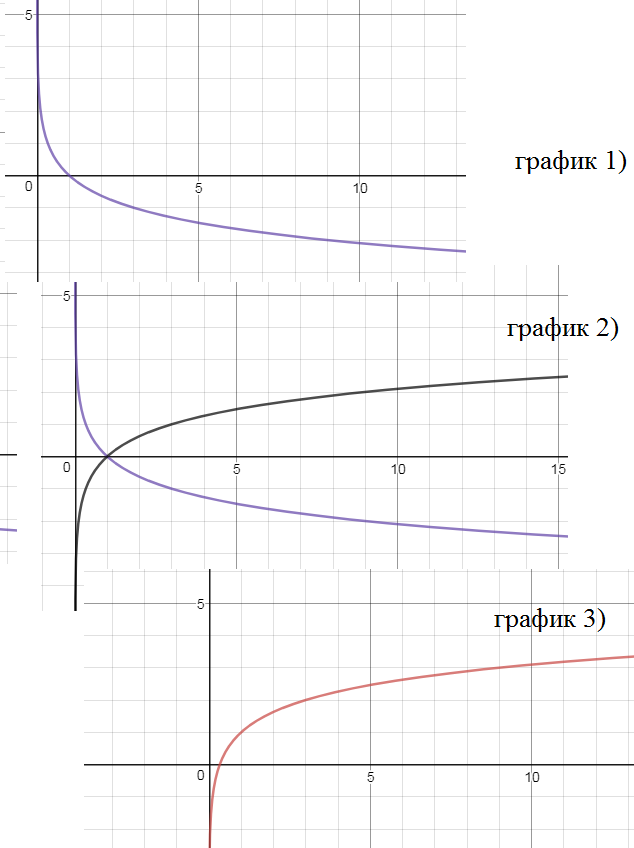
y=log_(1/3)x - см приложение 3 график 1)
y=-log_(1/3)x - зеркальное отражение первого относительно оси Ох
см там же график 2) черного цвета
y=-log_(1/3)x +1 - сдвиг на 1 единицу вверх
см. там же график 3)
г)
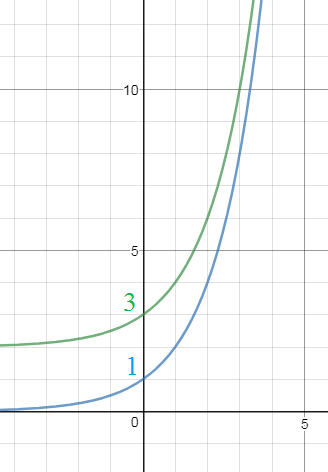
y=2^x - показательная функция с основанием 2, возрастающая на (- ∞ ;+ ∞ ) см. приложение 4 график синего цвета
y=2^(x) + 2 - сдвиг предыдущего графика на 2 единицы вверх
см. приложение 4, график зеленого цвета
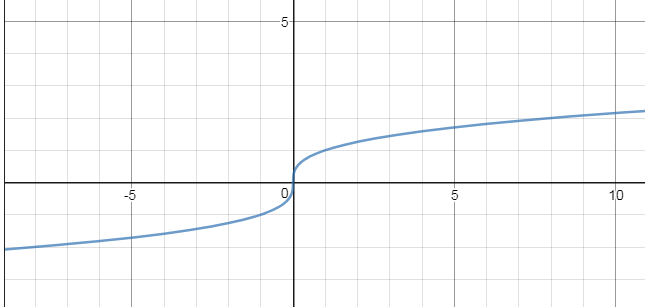
д)y=∛x
см. приложение 5
P.S
Если бы каждая задача была выставлена отдельно, получили бы гораздо быстрее более подробное решение и без всяких фраз типа ( см. приложение номер, рис.. ) на что было потрачено лишнее время.
См. запись на моей стене