Задача 33371 Задание на картинке...
Условие
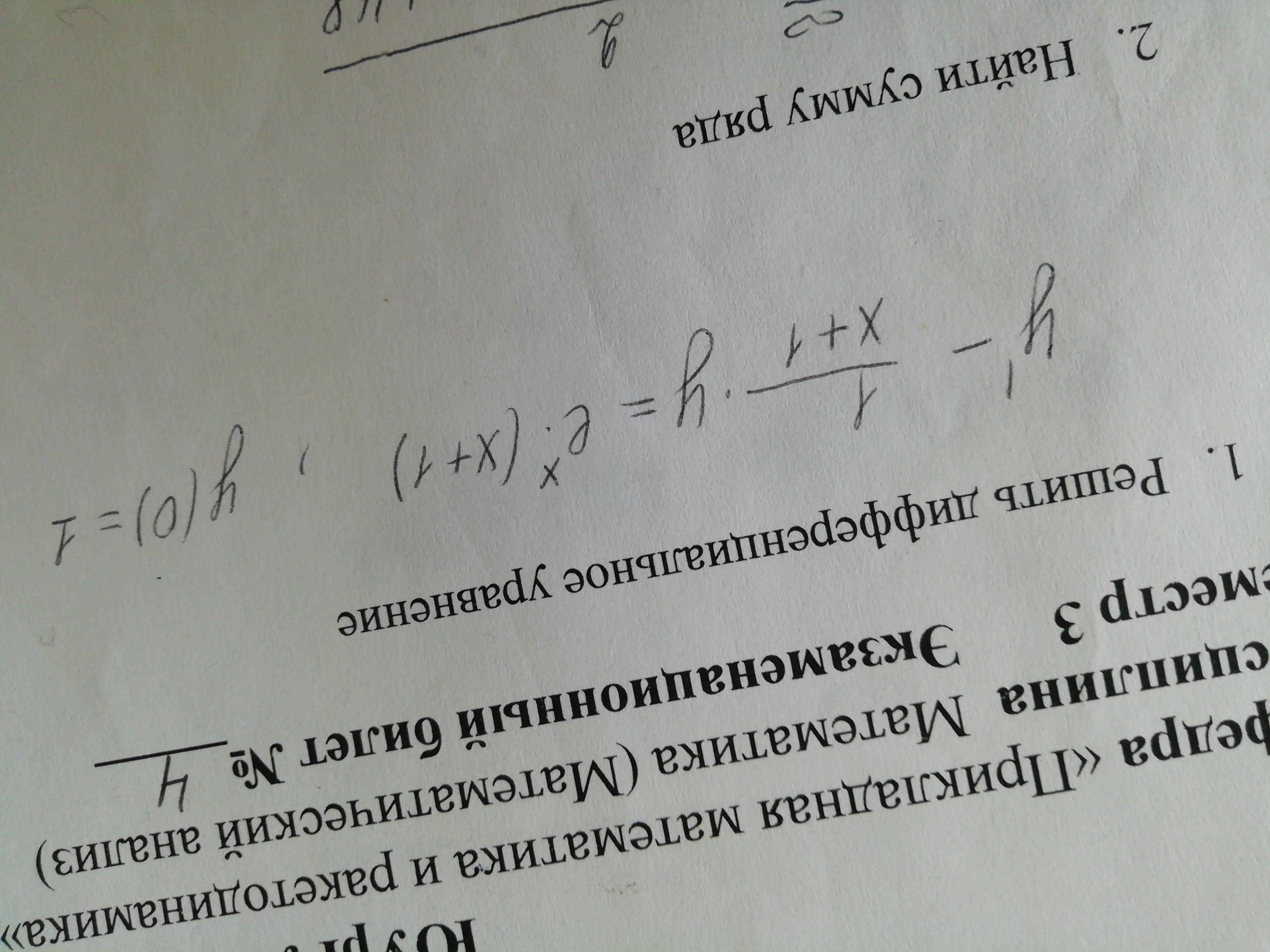
математика ВУЗ
474
Все решения
Находим y в виде произведения двух произвольный функций
y=u*v
y`=u`*v+u*v`
u`*v+u*v`-(1/(x+1))*u*v=e^(x)*(x+1)
u`*v + u*(v` - (1/(x+1))*v) = e^(x)*(x+1)
Функцию v выберем так, чтобы выражение в скобках равнялось 0
v`- (1/(x+1))*v=0
Тогда
u`*v +0=e^(x)*(x+1)
Решаем первое
Это уравнение с разделяющими переменными
dv/v=dx/(x+1)
ln|v|=ln|x+1|
v=(x+1)
подставляем во второе
u`*(x+1)=e^(x)*(x+1)
u`=e^(x)
u=e^(x)+C
y=u*v=(x+1)*(e^(x)+C)- общее решение
Находим частное решение
при х=0
у=1
1=(0+1)*(e^(0)+C)
1=1+C
C=0
y=(x+1)*e^(x) - частное решение
