Задача 33370 Задание на картинке...
Условие
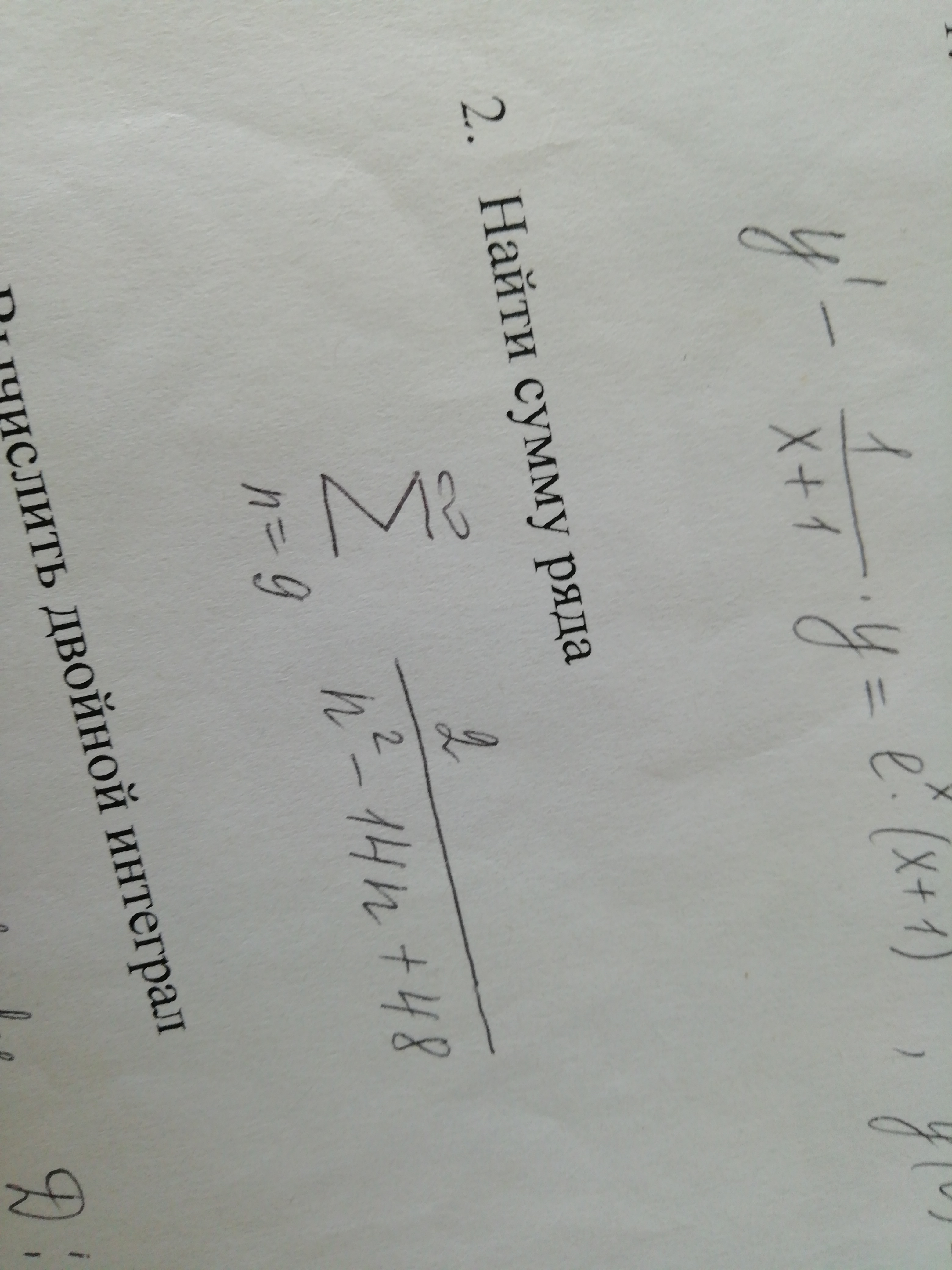
математика ВУЗ
407
Все решения
n2–14n+48=(n–6)(n–8)
а дробь на простейшие дроби
2/(n2–14n+48)=(1/(n–8))–(1/(n–6))
проверка
(1/(n–8))–(1/(n–6))=((n–6)–(n–8))/(n–6)(n–8)=2/(n2–14n+48)
Находим n–yю частичную сумму:
Sn=∑n9((1/(k–8)) –(1/(k–6)))=
=(1– (1/3)) + ( (1/2) – (1/4)) + ( (1/3) – (1/5)) + ((1/4) – ( 1/6))+...
+ (1/(n–10))–(1/(n–8)) + (1/(n–9)) – (1/(n–7)) + (1/(n–8)) + (1/(n–6))
= 1 +(1/2) – (1/(n–7)) + (1/(n–6))
По определению
S=limn→∞Sn=3/2
Обсуждения
