Задача 33315 ...

leten

2019-02-06 12:47:53

log(4-x) (28-3x-x^2) ≤ 1

x+7+...

sova

2019-02-06 13:27:15

★

ОДЗ:
{4-x >0 ⇒ x < 4
{4-x ≠ 1 ⇒ x ≠ 3
{28-3x-x^2 > 0 ⇒ x^2+3x-28 < 0; D=121; x=-7; x=4 ⇒ -7 < x < 4

x ∈ (-7;3)U(3;4)

Применяем метод рационализации
(4 - х - 1)*(28 - 3x - x^2 - 4 + x) ≤ 0

(3-x)*(-x^2 -2x+24) ≤ 0

x^2+2x-24=0
D=100
x=-6; x=4

(x-3)*(x+6)*(x-4) ≤ 0

Метод интервалов на ОДЗ уравнения:

(-7)_-__ [-6] __+___ (3) __-__ (4)

Решение (1)
(-7;- 6] U (3;4)

(2)
x^2-4x=3=(x-1)(x-3)

((x+7)*(x^2-4x+3) +14x-24 - 5*(x-3))/((x-1)(x-3)) ≥ 0

(x^3-4x^2+3x+7x^2-28x+21+14x-24-5x+15)/((x-1)(x-3)) ≥ 0

(x^3+3x^2-16x +12)/((x-1)(x-3)) ≥ 0

x=1 - нуль числителя, так ак 1+3-16=12=0
Выделим (х-1) в числителе:
x^3-x^2+4x^2-4x -12x+12=x^2*(x-1)+4x(x-1)-12*(x-1)=
=(x-1)*(x^2+4x-12)=(x-1)*(x-2)(x+6)

(x-1)(x-2)(x+6)/((x-1)(x-3)) ≥ 0

(x-2)(x+6)/(x-3) ≥ 0; x ≠ 1

_-__ [-6] ____+____ (1) _+__ [2] __-__(3) _+__

решение (2)
[-6;1) U(1;2] U(3;+ ∞)

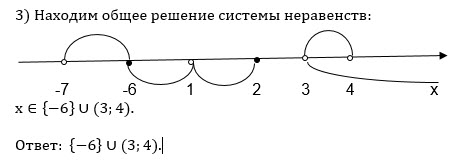
О т в е т. {-6} U(3;4)