Задача 33307 ...
Условие
4. ∫ (2x - √arcsin x) / √(1 - x^2) dx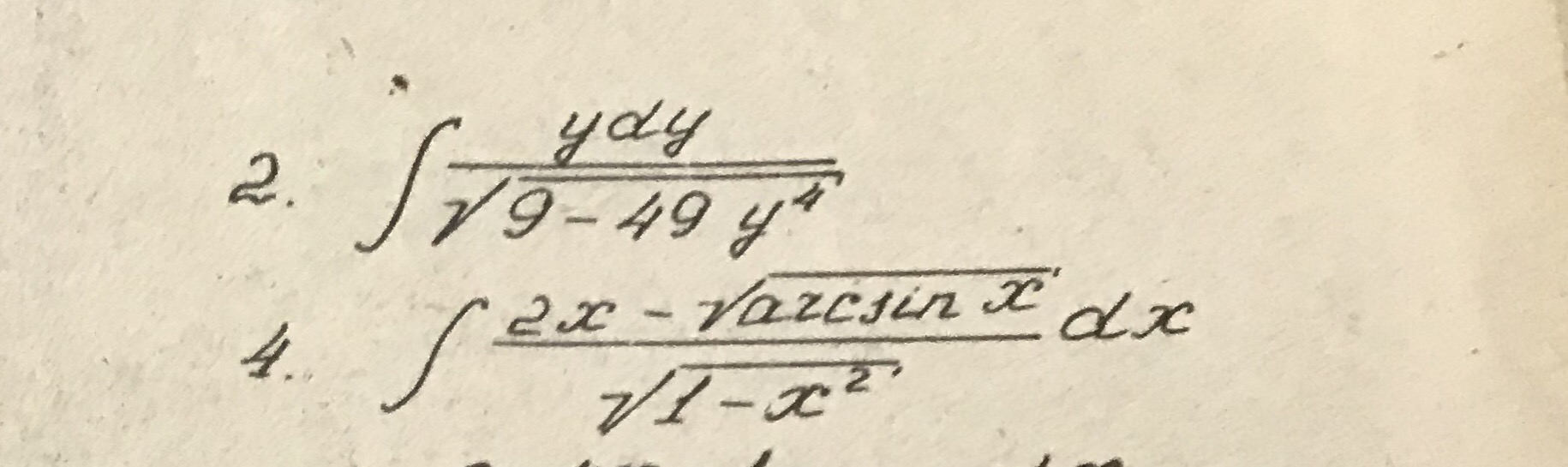
Решение
9-49y^4=3^2-(7y^2)^2
Замена
7y^2=t
dt=(7y^2)`dy
dt=14ydy
ydy=dt/14
Получаем табличный интеграл ( см 12)
(1/14) ∫dt/sqrt(3^2-t^2)= (1/14) arcsin(t/3) + C=
=(1/14)arcsin((7y^2)/3) + C
4.
Интеграл от суммы ( разности) равен сумме ( разности) интегралов.
= ∫ 2х/sqrt(1-x^2) - ∫ sqrt(arcsinx)/sqrt(1-x^2)dx
первый интеграл табличный (формула 2)
замена
1-x^2=t
dt=(1-x^2)`dx
dt=-2xdx
2xdx=-dt
∫2х/sqrt(1-x^2) = ∫ (-dt)/sqrt(t)= - ∫ t^(-1/2)dt= - t^((-1/2)+1)/((-1/2)+1)+C_(1)=
= - 2sqrt(t)+C_(1)= -2 sqrt(1-x^2) + C_(1)
второй интеграл табличный ( формула 2)
замена
arcisnx=u
du=(arcsinx)`dx
du=dx/sqrt(1-x^2)
∫ sqrt(arcsinx)/sqrt(1-x^2)dx= ∫sqrt(u)du= ∫ u^(1/2)du=
=u^((1/2)+1)/((1/2)+1) + C_(2)= u^(3/2)/(3/2) + C_(2)=
=(2/3) arcsinx*sqrt(arcsinx) + C_(2)
О т в е т. - 2 sqrt(1-x^2) +(2/3) arcsinx*sqrt(arcsinx) + C 