Задача 33284 ...
Условие
отрезке
y = x + sin 2x, [0,π/3].
2.С помощью правила Лопиталя вычислите предел функции.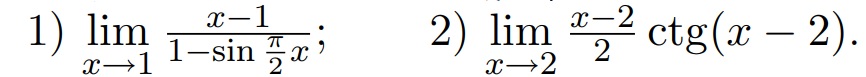
Решение
y`=1+cos2x*(2x)`=1+2cos2x
y`=0
1+2cos2x=0
cos2x=-1/2
2x= ± arccos(-1/2)+2πn, n ∈ Z
2x= ± (2π/3)+2πn, n ∈ Z
x= ± (π/3)+πn, n ∈ Z
Во внутренних точках отрезка [0;π/3]
производная не обращается в 0
y` имеет один и тот же знак, положительный.
Значит функция возрастает на отрезке и наименьшее значение принимает при х=0
y=0
Наибольшее значение в точке x=π/3
y=(π/3)+sin(2π/3)=(π/3)+sqrt(3)/2
2
Имеем неопределенность (0/0)
Применяем правило Лопиталя
1)
lim_(x→1)(x-1)`/(1-sin(π/2)x)`=lim_(x→1)(1)/(-cos(π/2)x)*(π/2)=
=(2/π*0)= ∞
2)
lim_(x→2)((x-2)/2)/(tg(x-2))=(0/0)=
=lim_(x→2)((x-2)/2)`/(tg(x-2))`=
=lim_(x→2)(1/2)/(1/cos^2(x-2))=(1/2)
