Задача 33282 ...
Условие
предмет не задан
492
Решение
★
5^(x)=t
t>0
25t+(2/t) ≤ 51
25t^2-51t+2 ≤ 0
D=(-51)^2-4*25*2=2601-200=2401=49^2
t=1/25 или t=2
1/25 ≤ 5^(x) ≤ 2
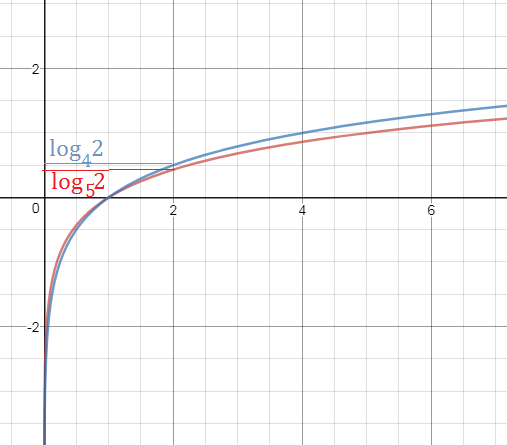
-1 ≤ x ≤ log_(5)2
log_(5)2 < log_(4)2=1/2
(2)
{x>0
{2x ≠ 1 ⇒ x ≠ 1/2
x ∈ (0;1/2) U(1/2;+ ∞ )
log_(2)(0,25)/log_(2)(2x) ≥ log_(2)(2^5*x) -1;
-2/(1+log_(2)x) ≥5+log_(2)x -1
log_(2)x=u
(u^2+5u+6)/(u+1) ≤ 0
_-__ [-3] _+__ [-2] _-__ (-1) _+__
log_(2)x ≤ -3 или -2 ≤ log_(2)x < - 1;
0 < x ≤ 1/8 1/4 ≤ x < 1/2
О т в е т. (0; 1/8) U (1/4; log_(5)2]