Задача 33215 Найти общее решение дифференциального...
Условие
1) ydx-(2sqrt(x^2+y^2)+x)dy=0
2) ((x+2y)dx+ydy)*(x+y)^(-2)=0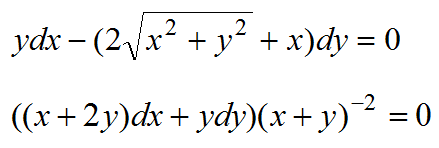
Решение
P(x;y)dx+Q(x;y)dy=0,
где P(x;y) и Q(x;y) - первой степени однородности ( k=1)
P( λx; λy)= λ ^(k)P(x;y)
Решают заменой
y/x=u ⇒ y=x*u
dy=xdu+udx
Подставляем y и dy в уравнение
1.
x*udx=(2sqrt(x^2+x^2u^2)+x)*(xdu+udx);
x*udx=х*(2sqrt(1+u^2)+1)*(xdu+udx)
делим на х
udx=(2sqrt(1+u^2)+1)*xdu+(2sqrt(1+u^2)+1)udx
u*(1-2sqrt(1+u^2)-1)dx=(2sqrt(1+u^2)+1)*xdu- уравнение с разделяющимися переменными
dx/x = (du/u)*(- 1- (1/(2sqrt(1+u^2)))
Интегрируем
∫ dx/x = (- ∫ du/u)-(1/2) ∫ du/(u*sqrt(1+u^2)
∫ du/(2u*sqrt(1+u^2)= замена переменной
1/u=t
u=1/t
du=-dt/t^2
sqrt(1+(1/t)^2)=sqrt(1+t^2)/t
⇒
∫ du/(u*sqrt(1+u^2)= -∫dt/sqrt(t^2+1)=-ln|t+sqrt(t^2+1)|
ln|x|=-ln|u|+(1/2)ln|1/u+ sqrt((1/u)^2+1)| + lnC,
ln|x|+ln|u|=ln C*|sqrt((1/u)+sqrt((1/u)^2+1))|
xu=C*sqrt((1/u)+sqrt(1/u)^2+1)),
где
u=y/x
y=C*sqrt((x/y)+sqrt((x/y)^2+1) - о т в е т.
2.
(x+2xu)dx+xu*(udx+xdu)=0
(x+2xu+xu^2)dx+x^2udu=0
x*(1+2u+u^2)dx= - x^2*udu
Делим на х
(1+2u+u^2)dx=-xudu - уравнение с разделяющимися переменными
dx/x=-udu/(u+1)^2
Интегрируем
∫ dx/x =- ∫ (u+1-1)du/(u+1)^2
∫ dx/x =- ∫ du/(u+1) + ∫ du/(u+1)^2
ln|x| = - ln|u+1| -(1/(u+1))+ C
ln|x|+ln|u+1|=-1/(u+1) + C
u=xy
ln|x*(xy+1)|=-1/(xy+1)+C - о т в е т.