Задача 33020 ...
Условие
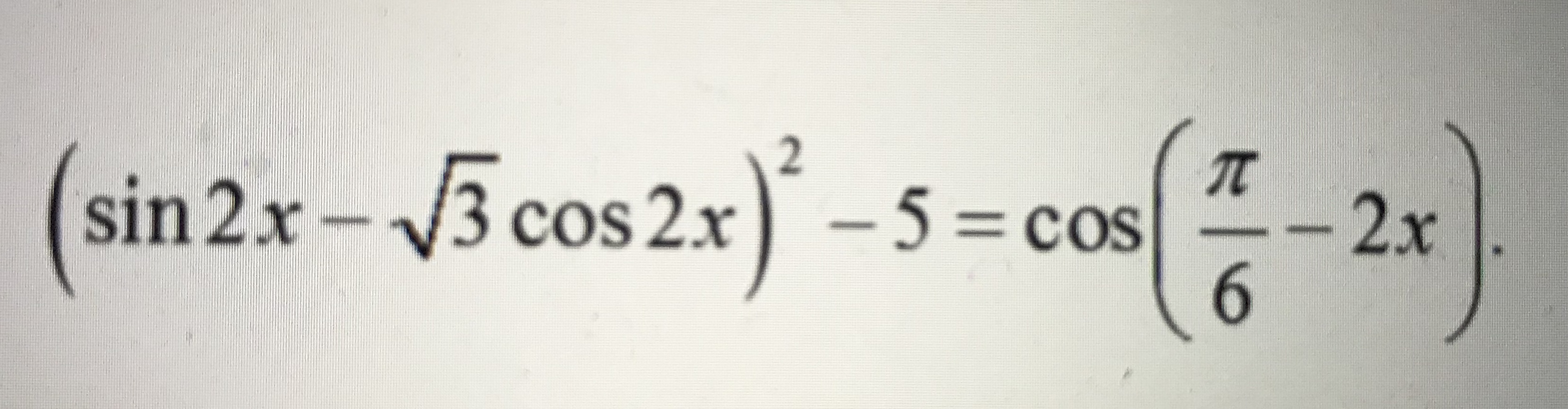
математика 10-11 класс
654
Решение
★
по свойству четности косинуса.
sin2x-sqrt(3)cos2x=2*((1/2)*sin(2x)-(sqrt(3)/2)*cos2x)=
=2*(cos(π/6)*sin2x- sin(π/6)*cos2x)=2*(sin(2x-(π/6))
Тогда
(sin2x-sqrt(3))^2=4*sin^2(2x-(π/6))=4*(1-cos^2(2x-(π/6)))
4 - 4 cos^2(2x-(π/6)) -5 -cos(2x-(π/6))=0
4cos^2(2x-(π/6)) + cos(2x+(π/6)) +1=0
D= 1 -4 * 4 < 0
Уравнение не имеет корней.