Задача 33011 (1 point) Прямая задана...
Условие
Прямая задана координатно-параметрическими уравнениями x = 1 + 7t, y = 2 + 3t, z = 3 + 6t. Вторая прямая параллельна первой и проходит через точку Р(5,5,3).
Найдите точки пресечения второй прямой с координатными плоскостями:
с плоскостью xy: ( , , ),
с плоскостью xz: ( , , ),
с плоскостью yz: ( , , ).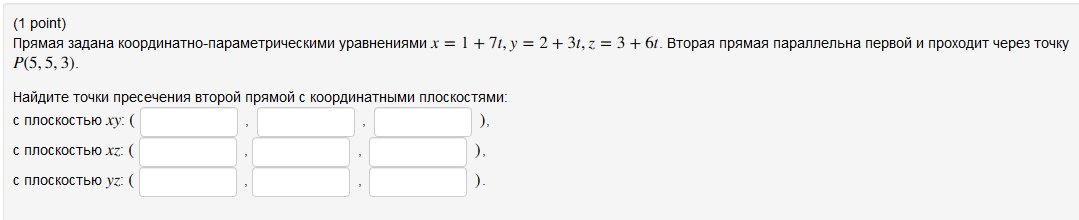
Решение
t=(x-1)/7;
t=(y-2)/3
t=(z-3)/6
Приравниваем
(x-1)/7=(y-2)/3=(z-3)/6 - данная прямая
Направляющий вектор этой прямой vector{s}=(7;3;6)
Параллельные прямые имеют одинаковые (коллинеарные) направляющие векторы
Составляем уравнение прямой, проходящей через точку Р с направляющим вектором vector{s}=(7;3;6)
(x-5)/7=(y-5)/3=(z-3)/6
Находим точку пересечения с плоскостью хОу
{z=0
{(x-5)/7=(y-5)/3=(z-3)/6
(x-5)/7=(0-3)/6
x-5=(-7/2)
x=3/2=1,5
(y-5)/3=(0-3)/6
y-5=-3/2
y=7/2=3,5
(1,5; 3,5; 0)
Находим точку пересечения с плоскостью хОz
{y=0
{(x-5)/7=(y-5)/3=(z-3)/6
(x-5)/7=(0-5)/3
x-5=(-35/3)
x=-20/3
(z-3)/6=(-5)/3
z-3=-10
z=-7
(-20/3;0;-7)
Находим точку пересечения с плоскостью yОz
{x=0
{(x-5)/7=(y-5)/3=(z-3)/6
(y-5)/3=(0-5)/7
y-5=(-15/7)
y=20/7
(z-3)/6=(0-5)/7
z-3=-30/7
z=-9/7
(0; 20/7; -9/7)