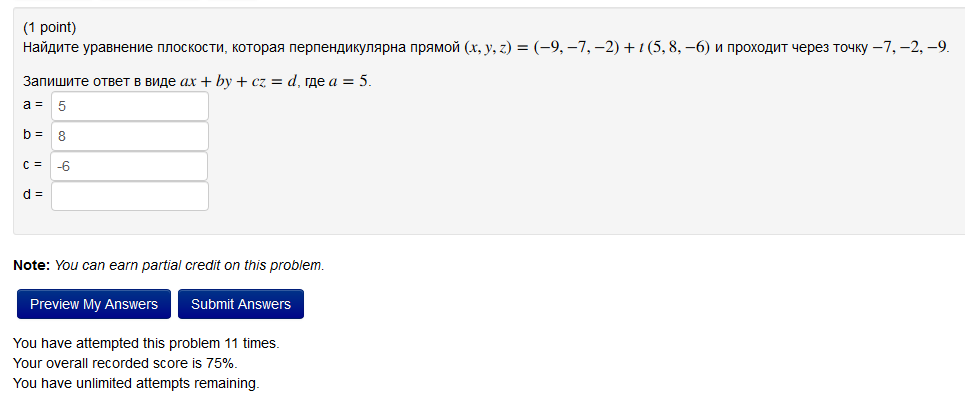
Задача 33007 (1 point) Найдите уравнение плоскости,...

kamilsai

2019-01-25 05:42:46

(1 point)
Найдите уравнение плоскости, которая перпендикулярна прямой (x, y, z) = (-9, -7, -2) + t (5, 8, -6) и проходит через точку -7, -2, -9.
Запишите ответ в виде ax + by + cz = d, где a = 5.
a = 5
b =
c =
d =

sova

2019-01-25 10:20:18

Направляющий вектор прямой vector{s}=(5;8;-6) становится нормальным вектором плоскости vector{n}=vector{s}=(5;8;-6)
Составляем уравнение плоскости, проходящей через точку
M_(o)(-7;-2;-9) c заданным нормальным вектором vector{n}=(5;8;-6)
5*(x - (-7)) + 8*(y - (-2)) - 6*(z - (-9))=0
5x +8y - 6z = 3
a=5
b=8
c=-6
d=3