Задача 32984 Найдите уравнение плоскости, которая...
Условие
-10x + 10y + 6z = -8 и проходит через точку -9, -3, -1.
Запишите ответ в виде ax + by + cz = d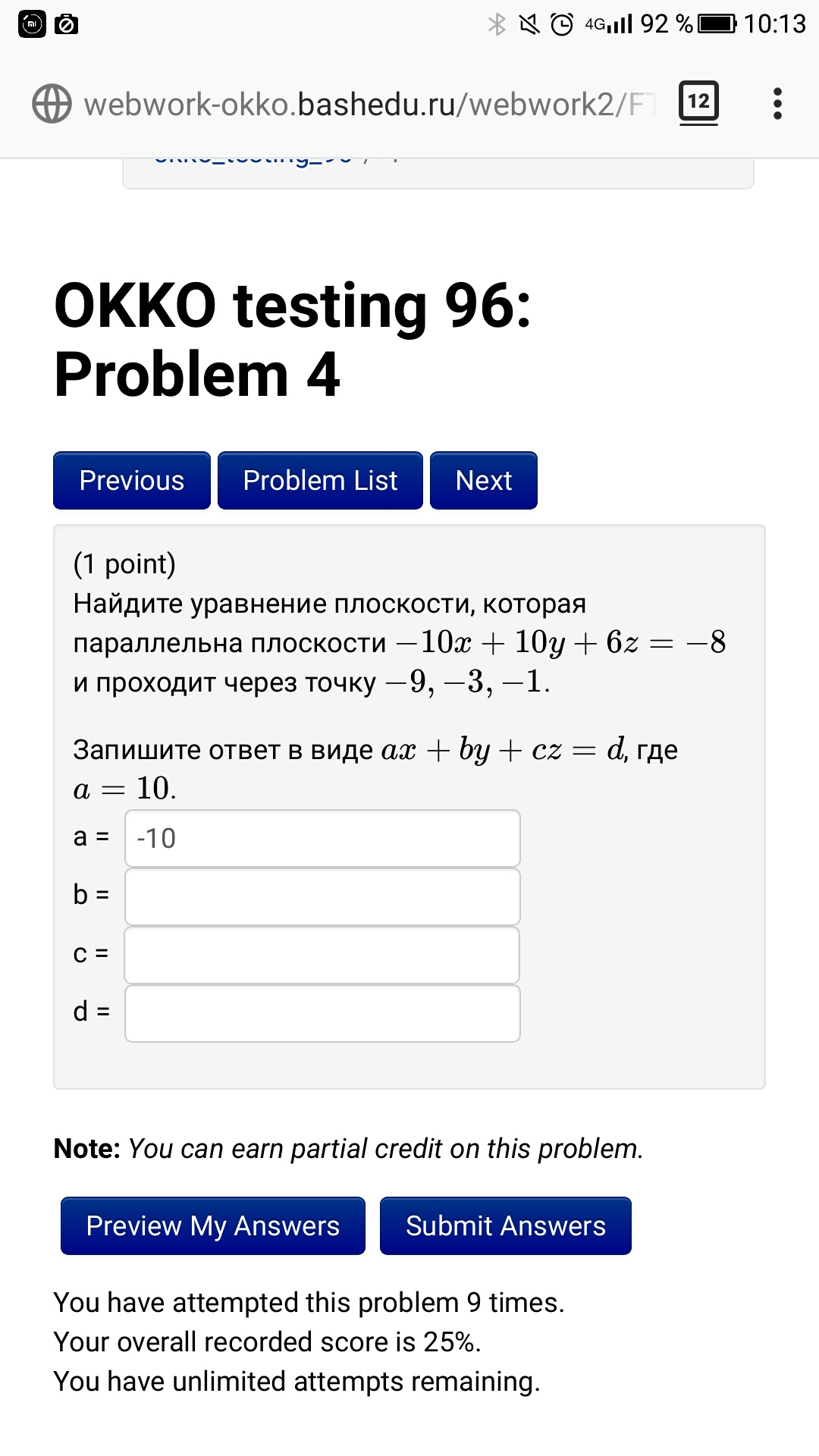
математика
629
Решение
★
Нормальный вектор данной плоскости vector{n}=(-10;10;6)
Уравнение плоскости, проходящей через точку (-9;-3;-1) с заданным нормальным вектором vector {n}=(-10;10;6)
-10*(x-(-9)) +10*(y-(-3))+6*(z-(-1))=0
-10x+10y+6z-54=0
Умножаем на (-1):
10х-10y-6z=-54
a=10
b=-10
c=-6
d=-54
