Задача 32937 ...

vk279109682

2019-01-23 10:03:06

1. Дан треугольник ABC. MB ⊥ ABC, MC ⊥ AC, AC = n, BC = m.
Найти длину AB.

2. Прямая AC - наклонная к плоскости α. Найти угол между прямой AC и плоскостью α, если A лежит в плоскости α, расстояние от C до A равно 16 см, а от C до плоскости α равно 8√3 см.

3. В треугольнике ABC сумма углов А и В равна 90°. Из точки А к плоскости α, в которой лежит сторона ВС треугольника, проведен перпендикуляр AO. Докажите, что прямая ВС перпендикулярна к плоскости СОА.

4. Сторона правильного треугольника ABC равна 5√3 см. Точка K не лежит в плоскости треугольника, причем КА = KB = KC = 10 см. Найти угол между прямой KV и плоскостью треугольника.

sova

2019-01-23 11:33:20

1.
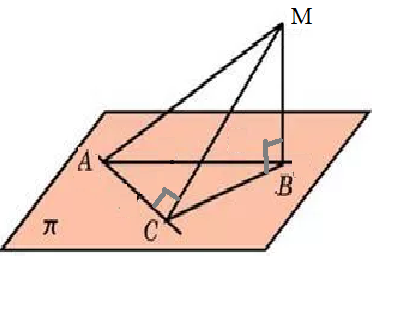
MB ⊥ плоскости АВС, значит перпендикулярна любой прямой лежащей в этой плоскости, в том числе и ВС
MC - наклонная,
ВС - проекция
По теореме о трех перпендикулярах,
если MC ⊥ AC, то и BC ⊥ AC
Δ ABC - прямоугольный, ∠ С=90 градусов.
По теореме Пифагора
АВ=sqrt(m^2+n^2)