Задача 32911 ...
Условие
4) lim (x→3) [ (√(x + 4) - 1) / (³√(3 - 2x - 3)) ]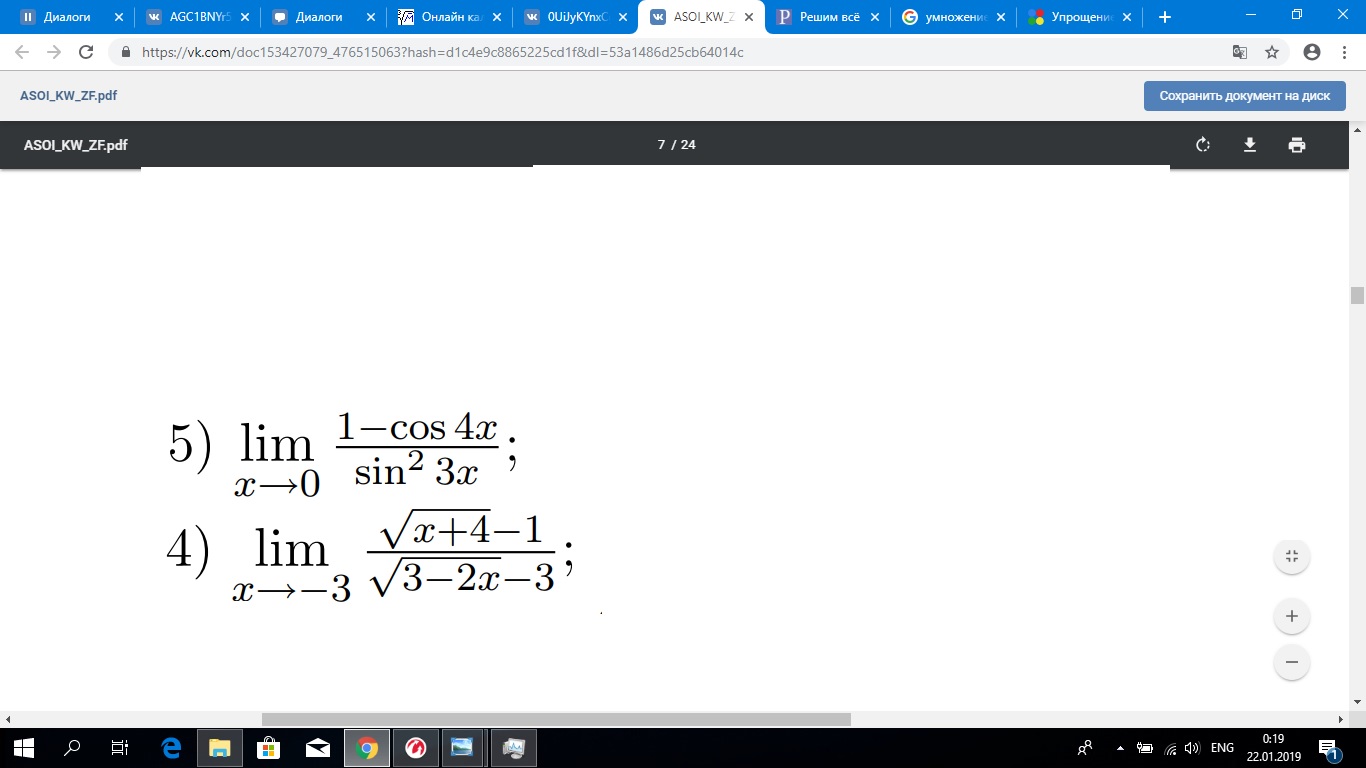
математика ВУЗ
835
Все решения
1-cos4x=2sin^22x
lim_(x→0) (2sin^22x)/sin^23x=(2*2*2)/(3*3)=8/9
lim_(x→0)(sin2x/2x)=1
lim_(x→0)(3x/sin3x)=1
4)
Неопределенность 0/0
Умножаем и числитель и знаменатель
на (sqrt(x+4)+1)*(sqrt(3-2x)+3)
Применяем формулу (a-b)(a+b)=a^2-b^2:
(sqrt(x+4)-1)*(sqrt(x+4)+1)=(sqrt(x+4))^2-1^2=(x+4-1);
(sqrt(3-2x)-3)*(sqrt(3-2x)+3)=(sqrt(3-2x))^2-3^2=(3-2x-9);
=lim_(x→ - 3)(x+4-1)*(sqrt(3-2x)+3)/(3-2x-9)*(sqrt(x+4)+1)=
=lim_(x→ - 3)(x+3)*(sqrt(3-2x)+3)/(-2*(x+3))*(sqrt(x+4)+1)=
сокращаем на (х+3)
=6/(-2*2)=-3/2
