Задача 32812 Написать уравнение касательной к кривой:...

vk390991176

2019-01-19 04:31:04

Написать уравнение касательной к кривой: y=sqrt(x)-2, зная, что эта касательная перпендикулярна прямой 4x - у = 0.

sova

2019-01-19 16:08:31

★

Произведение угловых коэффициентов взаимно
перпендикулярных прямых равно (-1).

Прямая 4х-у=0 имеет угловой коэффициент k=4
Значит, угловой коэффициент касательной
k=-1/4
геометрический смысл производной в точке:
k(касательной)=f `(x_(o))

f(x)=sqrt(x) - 2
f `(x)= (sqrt(x) - 2)`=1/2sqrt(x)
f`(x_(o))=1/2sqrt(x_(o))

-1/4 = 1/2sqrt(x_(o))
[b]sqrt(x_(o))=-2[/b]

это уравнение не имеет решений.
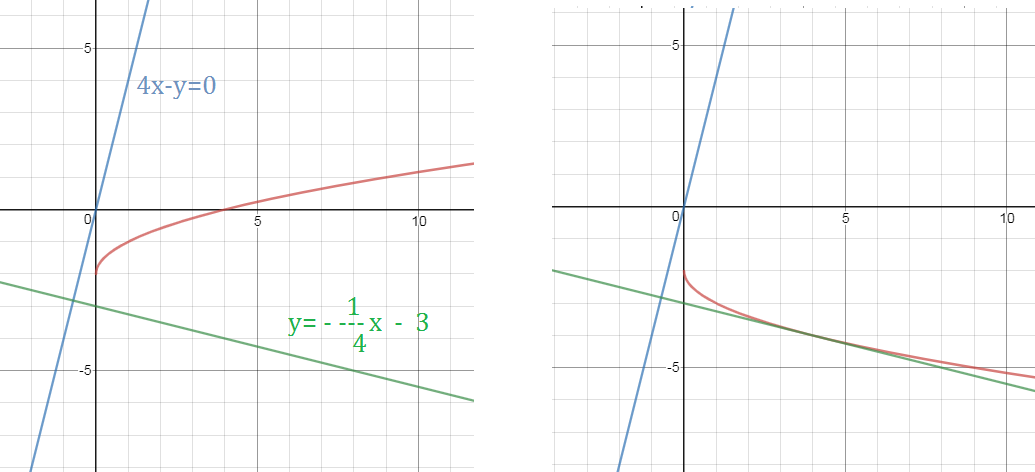
и на рисунке видно, что нельзя провести касательную с
угловым коэффициентом (-1/4),т.е. под тупым углом к оси ох


и фокус в том, что из y=sqrt(x)-2⇒
sqrt(x)=y+2
⇒ х=(y+2)^2 - парабола
и касательная, удовлетворяющая условию
у=(-1/4)х - 3 проходит в точке с абсциссой х_(о)=4 к другой ветви параболы
y=-sqrt(x)-2

Поэтому либо опечатка в условии
и должно быть y=-sqrt(x)-2
либо...
Уравнение касательной:
y - f (x_(o)) =f ` (x_(o))* (x - x_(o))

f(x)= - sqrt(x) - 2
f `(x)= ( - sqrt(x) - 2)`=- 1/2sqrt(x)
f`(x_(o))= - 1/2sqrt(x_(o))

-1/4 = - 1/2sqrt(x_(o))
[b]sqrt(x_(o))=2[/b]
x_(o)=4

f(4)=-sqrt(4)-2=-4
y - (-4)= -(1/4)*(x - 4) - уравнение касательной
y=(-1/4)x -3